LLM Transformer

Transformer (is all you need?)

Introduction

本文所有的内容和原始论文：Attention is All You Need的设计保持一致。Transformer最开始的论文（Attention is all you need）的任务其实是聚焦在Machine Translation上的，看摘要：

Our model achieves 28.4 BLEU on the WMT 2014 English-to-German translation task, improving over the existing best results, including ensembles, by over 2 BLEU. On the WMT 2014 English-to-French translation task, our model establishes a new single-model state-of-the-art BLEU score of 41.8 after training for 3.5 days on eight GPUs, a small fraction of the training costs of the best models from the literature.

Preliminaries

The dominant sequence transduction models are based on complex recurrent or convolutional neural networks that include an encoder and a decoder.

Attention Mechanism

See this blog for more info: Attention is all you need?

It will cover:

• Intuitive Attention Machnism: the basic design of key, value and query.

• Attention Pooling Algorithm: Calculate the correlation of each key and the query.

• Attention Scoring Function:

  • Masked Softmax Operation

  • Additive Attention

  • Scaled Dot-product Attention

• MultiHead Attention

• Self Attention

• Positional Encoding

Seq2Seq

问题的大背景是序列预测问题，即给定一个序列 $(x_1, x_2, \dots, x_n)$，每个词元 $x_i$ 可以被 embedding 成一个 d 维空间下的向量表示：$x_i \in \mathbb{R}^d$。

序列预测的目标就是输出 $(y_1, y_2, \dots, y_m)$，考虑相同的 embedding 方式，序列转导模型实现了输入矩阵向输出矩阵的线性变换。

$$M \in \mathbb{R}^{n \times d} \to \text{Sequence transduction models} \to N \in \mathbb{R}^{m\times d}$$

Encoder & Decoder Structure

传统的神经网络难以应对长度可变的序列输入，因此，主流的应对序列到序列的学习任务往往采用 Encoder - Decoder 的架构，而编码器和解码器的设计都依赖于循环神经网络的设计。

图节选自：Hands on DL: Encoder and Decoder

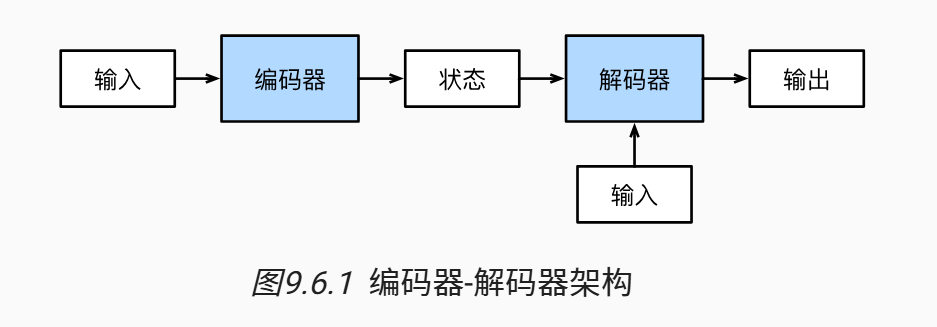
考虑传统的机器翻译任务，原始输入是待翻译的文本序列 $(x_1, x_2, \dots, x_n)$，这一部分会作为编码器的输入，编码器的任务是接受长度可变的输入编码为具有固定形态的编码状态（例如，一个矩阵），这一部分会作为将来解码器的输入之一。

解码器的另一部分输入来自于已经被翻译好的文本，例如考虑生成目标词元 $y_p$ 过程（$p \in [1,m]$），之前被翻译的 $(y_1, y_2, \dots, y_{p-1})$ 会被作为输入传递进解码器里面。传统的 Encoder Decoder的架构会使用循环神经网络作为内部的网络结构。

Encoder

编码器的重点在于处理长度可变的输入序列并将其转化为形状固定的上下文变量 $c$。在时间步 $t$，输入序列的第 $x_t$ 被输入进去，循环神经网络会施加循环层 $h_t = f(x_t, h_{t-1})$，得到对隐状态的更新，最终编码器会选定函数 $q$ 来实现对完整序列状态的编码：

$$c = q(h_1, h_2, \dots, h_n)$$

Decoder

解码器同样也是循环神经网络的状态设计，考虑时间步长为 $t^{\prime}$（为了和 $t$ 做区分），隐状态更新的公式如下：

$$s_{t^{\prime}} = g(y_{t^{\prime} - 1}, c, s_{t^{\prime} - 1})$$

之后再利用输出层的 softmax 操作获得最终的概率分布：

$$P(y_{t^{\prime}} | y_1, y_2, \dots, y_{t^{\prime} - 1}, \mathbf{c})$$

后续有关模型损失函数设计和训练细节的部分，详见循环神经网络的详细解读。

Bahdanau Attention

使用注意力机制的 seq2seq 的模型。

传统的依赖于循环神经网络建模的 Encoder - Decoder 的架构很难捕捉原有序列的序列信息（因为在解码器输出的过程中编码器获得的隐状态 $\mathbf{c}$ 是共有的，但是在不同的时间步长下，不同位置的词的重要程度是不一样的。）

例如，输入序列是 I like apple，目标序列是“我喜欢苹果”，在解码器输出“我”的时候和输出“苹果”时依赖相同的隐状态 $\mathbf{c}$，这样就会导致循环神经网络难以做较长的序列建模过程。

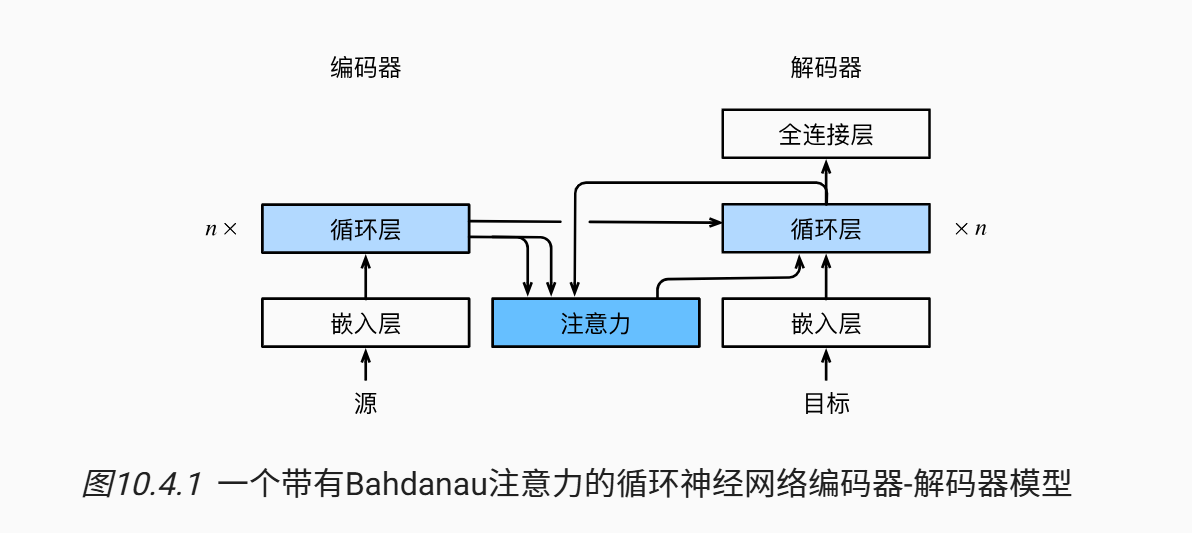
因此，在直觉上，我们希望隐藏层的输出 $\mathbf{h}_t$ 都能被利用（为了解码器的不同序列上的位置），而不仅仅是传入 $\mathbf{c} = q(\mathbf{h}_1, \mathbf{h}_2, \dots, \mathbf{h}_n)$ 作为上下文。

利用注意力机制可以做到这一点，在编码器和解码器的中间加入一个注意力机制，具体而言模型的设置如下：

• 原有序列 $(x_1, x_2, \dots, x_n)$ 仍然作为编码器的输入，编码器仍然使用循环神经网络建模，这一部分变化不大。

• 编码器除了输出 $\mathbf{c}$ 作为最终的编码隐状态，还会输出 $n$ 个键值对 $(\mathbf{h}_i, \mathbf{h}_i)$，作为键值对传入 Attention Module.

• 在解码器 RNN 中，考虑生成 $y_{t^{\prime}}$ 的过程，则注意力模块会将 $s_{t^{\prime} - 1}$ 作为 query 输入。

• Attention模块会输出一个 embedding, 这个embedding 和编码器的隐状态在相同的空间下（因为 Attention 的键值对都是编码器的隐藏状态序列），用公式表示就是：

$$\begin{split} \mathbf{c}_{t^\prime} = \sum^{n}_{t = 1} \alpha(\mathbf{s}_{t^{\prime}-1}, \mathbf{h}_t)\mathbf{h}_t \\ \mathbf{s}_{t^{\prime}} = g(y_{t^{\prime}}, \mathbf{c}_{t^{\prime}}, \mathbf{s}_{t^{\prime} - 1}) \end{split}$$

Model Architecture

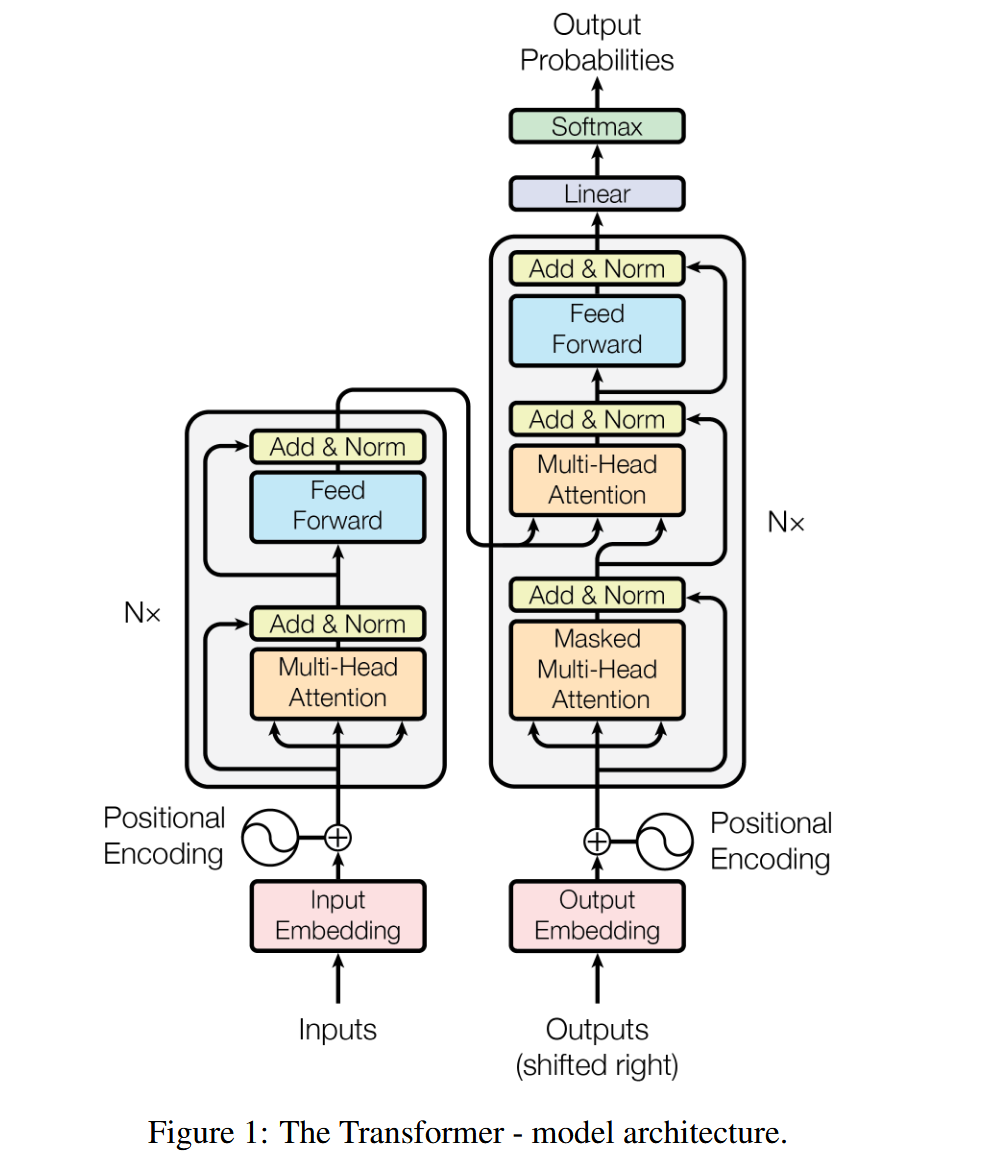
Overall Architecture

Transformer 的整体网络结构仍然保留了 Encoder-Decoder 的网络结构。相比于上文所涉及的添加注意力层的结构，Transformer 大胆地砍掉了循环神经网络的部分。Transformer 的编码器和解码器是基于自注意力的模块叠加而成的，源（输入）序列和目标（输出）序列的嵌入（embedding）表示将加上位置编码（positional encoding），再分别输入到编码器和解码器中。

因此输入是一个 $(\text{batch} \times \text{sequence length} \times \text{embedding dimension})$ 的三维张量，经过位置编码之后（Positional Encoding）之后进入编码器。而解码器会接受（目标序列的Embeddings）和编码器的输出，不过为了保证模型的正确性，Output Embeddings需要先做一个掩码（Masked），再进行输入。

在Transformer训练的过程中，是可以看到完整的目标序列的，但是我们希望Transformer不可以未卜先知，而是应该根据之前的内容做预测，因此会采用掩蔽矩阵来消除后续词的影响。

最终解码器经过一个Linear层调整size并通过softmax输出最终归一化的概率。

对于训练过程，目标序列y是已知的，因此我们需要使用掩码来防止模型在训练过程中未卜先知，只能利用之前的生成序列。而对应生成过程，我们不知道目标序列，因此需要模型根据自己之前的生成加上编码器的新的输出来做预测。

首先，其采用了类似于ResNet的堆叠模式（$N = 6$）。下面只对对一个单元层进行分析：

• 在Encoder部分，我们可以看到两个子模块，第一个子模块是Multi-Head Attention，第二个子模块是标准的全连接前馈神经网络。

• 不过在每一个子模块内，又加入了residual connection（ResNet）并且做了归一化的处理（LayerNorm）。

• 对于解码器也是类似的结构，不过加了一个Masked MultiHead Attention的结构来防止模型看到后面的预测序列。

Embeddings

模型的原始输入是一个个词元，每一个词元会根据单独训练的词表经过 embedding 的操作长成一个语义空间下的向量。不同语言的词表不一样，这并不是 Transformer 的重点。为了更方便的建模序列位置信息，在输入模块之前还加入了位置编码的过程。

Encoder

相比于传统的 Encoder 结构，Transformer 中的 Encoder 大胆了抛弃了循环神经网络的部分，而改用给予自注意力模式的 attention module。Encoder 部分的第一个子模块利用自注意力机制，用来学习输入文本的上下文信息（多头注意力可以聚焦到更加细节的特征学习上），接下来加入残差连接和归一化的操作。接下来第二个部分加入了一个两层的全连接神经网络，用来学习序列中的非线性部分。（因为缩放点积注意力是线性的，因此为了拟合非线性的特征，需要利用神经网络全连接层的激活函数实现这一点。）

Feed-forward Networks

用来学习非线性特征，使用 RELU 作为激活函数。

$$\text{FFN}(x) = \max(0, xW_1 + b_1)W_2 + b_2$$

Decoder

Decoder 的设置相对更加复杂，对于一个堆叠块内部：首先需要进入掩码自注意力模块，为了防止模型在训练时直接 Access 到后面的参考答案。在经过 Add & Norm 之后，进入第二个 Attention 模块，这个模块和之前的不同，不再是 Self-Attention，因为其 K, V 都来自于 Encoder 的输出序列，即 $(z_i, z_i)$ 会被作为 $n$ 个键值对进入这个注意力模块。

注意！$(z_i, z_i)$ 虽然还是在原有语义下的向量，但是已经通过编码器学习到了句子的上下文关系，这种上下文关系可以被用在翻译后的语言上，但是需要融合嵌入进翻译后语言的语义空间上。

经过这个注意力模块后，模型已经能够捕捉到句子的上下文了，但是还需要迁移到另一个语义空间中，因此后面还需要接一个前馈神经网络进行融合。

最后，经过一个线性层将特征投影到英文词表上，并做概率分布的 softmax 计算，最终就得到了输出 $y_{t^{\prime}}$ 的词汇的概率分布。

Normalization

在传统的神经网络中，归一化是非常关键的一步，这会为后续训练中的优化算法提供便利，防止出现梯度消失或者梯度爆炸的现象，提升稳定性。对于 Transformer 块，传入和传出的矩阵的维度为 $(\text{batches}, \text{sequence length}, \text{dimension})$。形式化地说，考虑输入 $X \in \mathbb{R}^{N \times L \times D}$:

• $N$ is the number of batches

• $L$ is the number of sequence length

• $D$ is the number of dimension

$$\forall x_{(n,l,d)} \in X, \ y_{(n,l,d)} = \gamma(\frac{x_{(n,l,d)} - \mu}{\sqrt{\sigma^2 + \epsilon}}) + \beta$$

• $x_{(n,l,d)}$ 是输入张量 $X$ 在批次 $n$、序列位置 $l$、维度 $d$ 上的原始值。

• $μ$ 是上下文相关的均值（context-dependent mean）。它的计算方式取决于我们选择在哪个维度或哪些维度上进行归一化。

• $σ^2$ 是上下文相关的方差（context-dependent variance）。它的计算方式与 $μ$ 类似，也取决于归一化的维度选择。

• $ϵ$ 是一个很小的正数，用于防止除以零，增加数值稳定性。

• $γ$ 是缩放因子（learnable scaling parameter）。它是一个可学习的参数，用于调整归一化后的数据的尺度。

• $β$ 是平移因子（learnable shifting parameter）。它是一个可学习的参数，用于调整归一化后的数据的偏移。

两个可学习的参数在比较简化的归一化中会被省略，即不带可学习参数的简单归一化版本（这一个版本也不考虑 $\epsilon$）：

$$\forall x_{(n,l,d)} \in X, \ y_{(n,l,d)} = \frac{x_{(n,l,d)} - \mu}{\sigma}$$

归一化的选择关键在于如何计算一个高阶张量的均值和标准差。

Batch Normalization

在批量归一化中，我们沿着 批次 ($N$) 和 序列长度 ($L$) 维度计算统计量，对每个 特征维度 ($D$) 进行归一化。
这意味着 $\mu$ 和 $\sigma^2$ 是针对每个特征维度 $d$ 计算的。

• 均值 $\mu_d$：

  $$\mu_d = \frac{1}{N \cdot L} \sum_{n=1}^N \sum_{l=1}^L x_{n,l,d}$$

• 方差 $\sigma_d^2$：

  $$\sigma_d^2 = \frac{1}{N \cdot L} \sum_{n=1}^N \sum_{l=1}^L (x_{n,l,d} - \mu_d)^2$$

• 缩放因子和平移因子： $\gamma$ 和 $\beta$ 也是针对每个特征维度 $d$ 独立的，即 $\gamma_d, \beta_d \in \mathbb{R}^{D}$。
  因此，对于每个 $x_{n,l,d}$：

  $$y_{n,l,d} = \gamma_d \left( \frac{x_{n,l,d} - \mu_d}{\sqrt{\sigma_d^2 + \epsilon}} \right) + \beta_d$$

BN 旨在解决“内部协变量漂移 (Internal Covariate Shift)”问题，即每个特征的分布在训练过程中不断变化。为了稳定这些分布，BN 必须知道哪些值属于同一个特征。这个“同一个特征”就是由 dimension 轴定义的。如果没有 dimension 的概念，BN 就无法区分哪些值应该一起被归一化以代表同一个特征的分布。它需要每个维度上的统计量来调整该维度上的所有数据点。

Layer Normalization

在层归一化中，我们沿着 特征维度 ($D$) 计算统计量，对每个 样本 ($N$) 和 序列位置 ($L$) 进行归一化。
这意味着 $\mu$ 和 $\sigma^2$ 是针对每个样本 $n$ 和每个序列位置 $l$ 计算的。

• 均值 $\mu_{n,l}$：

  $$\mu_{n,l} = \frac{1}{D} \sum_{d=1}^D x_{n,l,d}$$

• 方差 $\sigma_{n,l}^2$：

  $$\sigma_{n,l}^2 = \frac{1}{D} \sum_{d=1}^D (x_{n,l,d} - \mu_{n,l})^2$$

• 缩放因子和平移因子： $\gamma$ 和 $\beta$ 在所有样本和序列位置上共享，但通常也是与特征维度 $D$ 相同长度的向量，即 $\gamma, \beta \in \mathbb{R}^{D}$。
  因此，对于每个 $x_{n,l,d}$：

  $$y_{n,l,d} = \gamma_d \left( \frac{x_{n,l,d} - \mu_{n,l}}{\sqrt{\sigma_{n,l}^2 + \epsilon}} \right) + \beta_d$$

在 Transformer 等序列建模模型中，因为序列长度 $N$ 可变（并且是频繁变化），因此为了提升模型的鲁棒性，往往采用 Layer Normalization 的方式实现归一化。

Complexity: Why Self-Attention

在相同的 Encoder-Decoder 的基本架构下，为什么选择 Transformer 具有优势？笔者在这个部分从时间复杂度的角度探讨了这一点：

从形式化的角度去理解，编码器都完成了这样的一件事情：将输入序列 $(x_1, x_2, \dots, x_n)$ 编码，输出新的序列 $(z_1, z_2, \dots, z_n)$，这个序列应该包含原始文本的上下文信息，以便传递给解码器做输出。（编码编的码就是抽象的上下文信息），为了方便，这里认为 $x_i, z_i \in \mathbb{R}^{d}$。

时间复杂度的计算主要依赖于三个指标：

• Total computational complexity per layer (这一部分的时间复杂度主要在做的矩阵乘法以及矩阵的 size)

• Amount of computation that can be parallelized

• Path length between long-range dependencies in the network

Experiments & Results

一些训练细节的内容详见论文原文，此处不介绍。

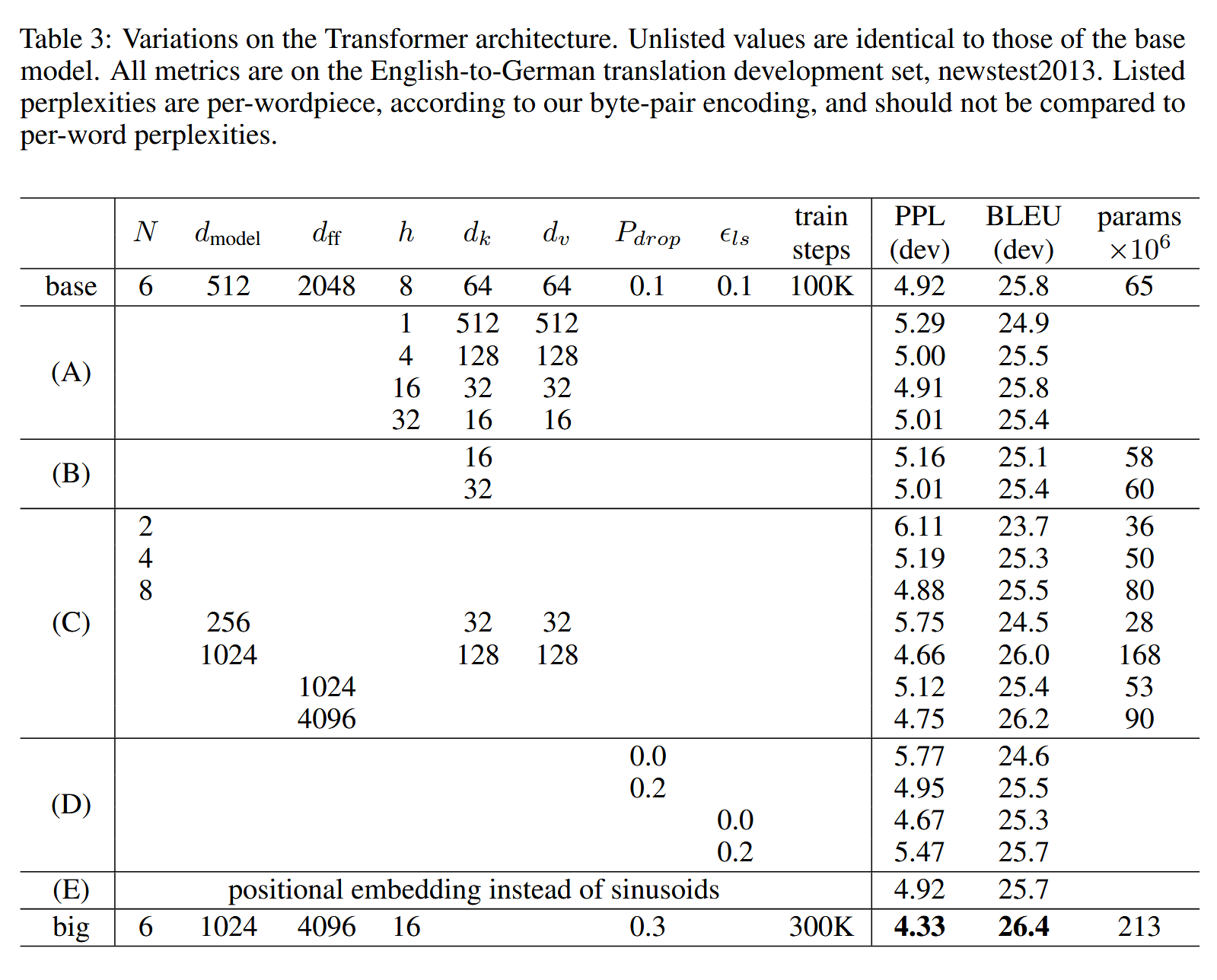
相关参数是：

• $N$: 堆叠 Transformer 块的数量

• $d_{\text{model}}$: Embedding dimension

• $d_{\text{ff}}$: 前馈网络的深度（前馈神经网络隐藏层的深度）

• $h$: number of multi heads

• $d_k$: Dimensions of keys, $d_k = \frac{d_{\text{model}}}{h}$，一个方面是为了学习特征，另一方面是为了拼接后保持一致。

• $d_v$: Dimensions of queries

• $P_{\text{drop}}$: Dropout rate

• $\epsilon_{\text{ls}}$: Label Smoothing

In Table 3 rows (B), we observe that reducing the attention key size dk hurts model quality. This suggests that determining compatibility is not easy and that a more sophisticated compatibility function than dot product may be beneficial. We further observe in rows © and (D) that, as expected, bigger models are better, and dropout is very helpful in avoiding over-fitting. In row (E) we replace our sinusoidal positional encoding with learned positional embeddings, and observe nearly identical results to the base model.

Conclusion

Attention is all you need!