Data Structure: Tree

The title image is from here.^[2]

Abstract

This article introduces the fundamental knowledge about tree data structures, including the key concept of hierarchy in trees, the strict standard definition of trees, and the declaration of abstract base classes. Additionally, the article discusses the role of trees and provides basic knowledge about binary trees.

Introduction

在上一章的学习中，我们聚焦于线性数据结构——线性表，其本质特征和定义是：数据元素之间按照线性关系进行排列。同时，我们对线性表做了一些约束，衍生出更加具体的数据结构：

• 从内存管理的视角进行约束

  • 链接实现

  • 顺序实现

• 从元素的进出次序的视角进行约束

  • 栈（LIFO）

  • 队列（FIFO）

  • 双端队列

• 对数据元素的类型进行约束

  • 字符串

我们是时候开启一段新的旅程了，线性表的威力固然强大，但是记住，数据结构的本质是抽象的建模过程，但是很多时候简单的线性结构并不能模拟这个复杂的世界。

例如，我的文件夹：

.
├── 1.md
├── 1.txt
├── 3.md
├── 4.md
├── 5.md
├── README.md
├── bar
├── example.sh
├── foo
├── project42
├── scripts.py
├── test
│   ├── a.py
│   ├── b.py
│   ├── c.py
│   ├── d.py
│   ├── e.py
│   ├── f.py
│   ├── folder1
│   │   └── README.md
│   ├── folder2
│   │   └── README.md
│   ├── folder3
│   │   └── README.md
│   ├── folder4
│   │   └── README.md
│   ├── folder5
│   │   └── README.md
│   ├── folder6
│   │   └── README.md
│   ├── folder7
│   │   └── README.md
│   ├── folder8
│   │   └── README.md
│   ├── folder9
│   │   └── README.md
│   ├── g.py
│   ├── h.py
│   ├── helloa.txt
│   ├── hellob.txt
│   ├── helloc.txt
│   ├── hellod.txt
│   ├── helloe.txt
│   ├── i.py
│   └── j.py
├── thefilefolder
│   ├── 1.md
│   ├── 1.py
│   ├── 2.md
│   ├── 2.py
│   ├── 3.md
│   ├── 3.py
│   ├── 4.md
│   └── 5.md
└── vimtest.txt

14 directories, 41 files
BASH

同理，对于许多具有等级划分或者结构层次的数据结构，线性表似乎显的有点无能为力。因此我们引入一种全新的数据结构：树，来刻画这样一种抽象关系。

Definition

为了方便展示，博客中的所有树状结构全部使用Mermaid流程图的形式。

我们首先展示一个简单的树形结构：

根据这个可视化的树，我们一句一句给出树的标准定义：

• 树是若干个节点的有限集合。

  • 这句话阐明了树的基本元素是节点。

  • 这是否也在暗示我们对于树的实现：链接貌似优于顺序？（后面再讨论）

• 它可以是空集，也可以是以下的结构：

  • 存在根节点

  • 其他的节点可分割为有限个互不相交的集合，这些集合本身也是一棵树。

第二句话十分的重要，因为它本质就是树后续递归操作的底层原理，或者说树的递归定义。

这句话有以下几种理解方式：

• 一棵树可以根据根节点不断的做分割，直到变成空集。（分割的视角）

• 一棵树根据层级的不同可以不断的向下延伸直到底部。（延伸的视角）

Fundamental terminology

术语	描述
节点 (Node)	树中的基本元素，包含数据和指向其他节点的链接。
根节点 (Root)	树的顶层节点，没有父节点。根节点唯一！
父节点 (Parent)	一个节点的直接上级节点。
子节点 (Child)	一个节点的直接下级节点。
叶子节点 (Leaf)	没有子节点的节点，也称为终端节点。
内部节点 (Internal)	至少有一个子节点的非根节点。
兄弟节点 (Sibling)	具有相同父节点的节点。
祖先节点 (Ancestor)	从根节点到该节点的路径上的所有节点。
后代节点 (Descendant)	从该节点到叶子节点的路径上的所有节点。
子树 (Subtree)	树中的任意节点及其所有后代节点构成的树。
深度 (Depth)	从根节点到该节点的路径长度。
高度 (Height)	从该节点到叶子节点的最长路径长度。树的高度是根节点的高度。
层次 (Level)	根节点为第1层，其子节点为第2层，以此类推。
度 (Degree)	节点的子节点数量。树的度是树中节点的最大度数。
路径 (Path)	从一个节点到另一个节点的节点序列。
森林 (Forest)	由若干棵互不相交的树组成的集合。
二叉树 (Binary Tree)	每个节点最多有两个子节点的树。
满二叉树 (Full Binary Tree)	每个节点都有0个或2个子节点的二叉树。
完全二叉树 (Complete Binary Tree)	除了最后一层，其他层都是满的，且最后一层节点尽量靠左的二叉树。
平衡二叉树 (Balanced Binary Tree)	左右子树高度差不超过1的二叉树。
二叉搜索树 (Binary Search Tree)	左子树节点值小于根节点，右子树节点值大于根节点的二叉树。
前序遍历 (Preorder Traversal)	先访问根节点，然后左子树，最后右子树。
中序遍历 (Inorder Traversal)	先访问左子树，然后根节点，最后右子树。
后序遍历 (Postorder Traversal)	先访问左子树，然后右子树，最后根节点。
层序遍历 (Level Order Traversal)	按层次从上到下、从左到右访问节点。

Fundamental Computations

树的基本逻辑关系是父子关系，或者说等级关系。以下是树的常见运算：

• create() : create a new tree.

• clear() : clear all nodes in a tree.

• isEmpty() : judge whether a tree is clean.

• root() : find the value of the root node.

• parent(x) : find the parent value of node x.

• child(x, i) : find the ith child value of node x.

• remove(x, i) : remove the ith child subtree of node x.

• travese() : traverse all the nodes in the tree.

//Abstract class 
template <class T>
class Tree{
    public:
        virtual void create() = 0;
        virtual bool isEmpty() const = 0;
        virtual T root(T invalid_flag) const = 0;
        virtual T parent(T current_node, T invalid_flag) const = 0;
        virtual T child(T current_node, int tree_index, T invalid_flag) const = 0;
        virtual void remove (T current_node, int tree_index) = 0;
        virtual void traverse () const = 0;

};
CPP

注意的是，函数声明中的invalid_flag是针对找不到根节点，找不到父节点或者找不到子节点而设计的。

What’s Next？

我们来想想具体如何实现树形结构，貌似有一点复杂，因为树的结构本身比较复杂，更不用提插入、删除、翻转节点这类更加复杂的操作了。因此，我们从最简单的情形出发：即一个节点至多延伸出两个子节点。

我们把这种树定义为二叉树，另一种递归的定义方式：一个树或者为空，或者由一个根节点及两颗互不相交的子树构成。而子树也是二叉树。

例如上面的树很明显不是一个二叉树，因为Me有三个儿子。如果老三不存在，那就是一颗比较完美的二叉树（满二叉树）：

关于二叉树我们会在下一篇文章中详细讨论。

彩蛋：当你学习完二叉树的时候，记得回来看一看，一定会对树有着更深的认识和见解！

Tree and Forests

请务必在学习完二叉树的基本知识之后再来学习本章。

广义树的存储实现

在二叉树中，孩子的个数和种类是具有严格规定的，只有左儿子和右儿子并且需要严格区分。但是对于一般的树而言，孩子的数目是不固定的，节点可以有很多个子节点，也可以没有子节点。因此，此时采用二叉树的广义存储结构会显得非常赘余，因为节点的儿子数可以动态改变。因此，我们需要探寻一种新的可以存储广义树的节点存储方式。下面介绍孩子链表示法和孩子兄弟表示法，以及其对应的遍历顺序。

孩子链表示法

我们从块状链表的思想优化广义树的存储实现。因此，可以把每个结点的所有孩子组织成一个链表，结点的设置可以优化为：

• 储存数据的data
• 指向孩子链的指针

如果我们把树的所有节点全部放进一个数组中，这个就是广义树的静态存储。也可以组织成一个链表（那就是块状链表），那就是动态的孩子链表。此外，我们也可以在表头数组中额外添加一个存储父节点位置的字段，称为带双亲的孩子链表示法。

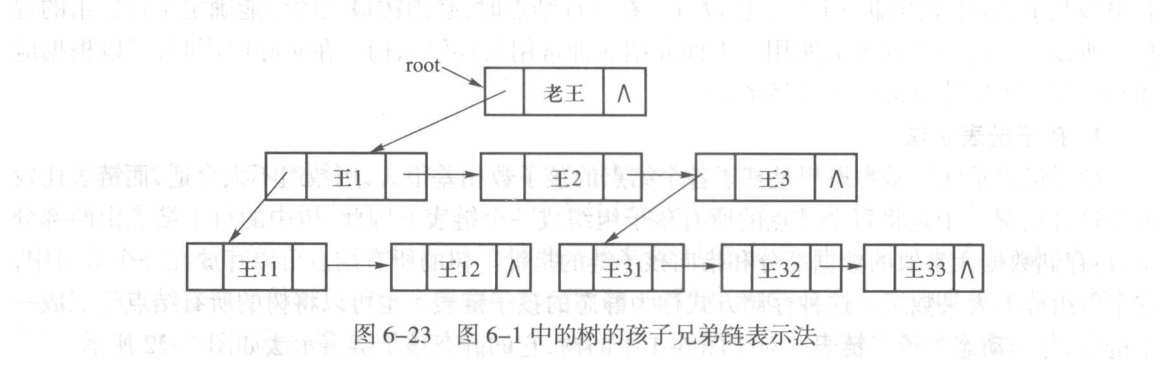
孩子兄弟链表示法

在孩子链表示法中，我们在本质上只是使用数组存储每一个结点，但优化了有关孩子的存储。我们可以换一种思路，使用二叉树来表示广义树：

• 左指针指向孩子链表
• 右指针指向兄弟链表

这样的存储让树的结构更加的清晰，让不同层级（高度）的结点可以快速找到子节点。同时，其与二叉树的联结更加紧密，树本质上还是二叉树的形态。

child and brothers

双亲表示法

一个爸爸可以有很多儿子，但是一个儿子只能有一个爸爸！在双亲表示法中，我们只需要储存对应节点的父亲节点即可成功建树。使用双亲表示法能够快速上升到根节点，但是无法下降到叶子结点。

森林

Definition：树的集合 & 树的序列

在哈夫曼算法中，对于集合中的数不断归并的过程也可以算作是森林的归并形式！

因此，对于森林，我们考虑将森林转化成一整颗二叉树的过程：

• 将每棵树转换成对应的二叉树，得到二叉树的集合。（使用孩子兄弟链的表示）
• 将$B_i$作为$B_{i-1}$作为根节点的右节点，使数不断延伸。

为什么需要这样做？这与孩子兄弟链表示法有关，在孩子兄弟链的生成过程中，根节点没有兄弟，因此根节点的右节点始终为空。我们可以使用这个位置的空缺来连接上新的二叉树，实现二叉树对森林高效存储。

如果需要从二叉树反解码成森林，我们可以从根节点开始不断移动到右子节点并且不断拆分成每一棵子树。

Applications

这篇文章^[1]详细的介绍了树形结构的相关应用，总结一下就是：

树的主要用途和应用场景包括：

1. 存储层次化数据：如文件系统、DOM模型、DNS系统等，这些数据天然具有层次结构。
2. 高效的搜索：二叉搜索树等树结构可以在对数时间内完成搜索，比线性数据结构更高效。
3. 排序：自平衡二叉搜索树等可以在插入数据时自动排序，方便查找最小、最大值等。
4. 动态数据管理：树结构可以动态增长和收缩，适合数据频繁变化的场景，如实时系统。
5. 高效的插入和删除：树结构提供了高效的插入和删除算法，适合需要频繁增删数据的应用。
6. 易于实现：相比图等复杂数据结构，树结构相对容易实现，广泛应用于编程项目中。

其他应用场景包括：

• 存储层次化数据：如文件夹结构、组织架构、XML/HTML数据等。
• 二叉搜索树：用于快速搜索、插入、删除排序数据。
• 堆：用于实现优先队列。
• B树和B+树：用于数据库索引。
• 语法树：用于编译器设计中的代码扫描、解析和表达式求值。
• K-D树：用于组织K维空间中的点。
• Trie树：用于实现字典的前缀查找。
• 后缀树：用于快速模式搜索。
• 生成树和最短路径树：用于计算机网络中的路由器和网桥。
• 决策树：用于人工智能中的决策算法。
• 组织结构图：用于大型组织的层级结构。
• XML解析器：用于解析XML文档。
• 机器学习算法：如决策树算法。
• 数据库索引：用于高效的数据检索。
• DNS服务器：用于域名解析。
• 计算机图形学：用于图像合成和视觉效果。
• 表达式求值：用于计算算术表达式。
• 游戏算法：如象棋游戏中的防守走法存储。
• Java虚拟机：用于管理和组织数据。

Tree is so important!

References

1. Applications of tree data structure - GeeksforGeeks ↩
2. Invert a Binary Tree ↩