DataStructure-Stack

数据结构——栈

Abstract

Definition

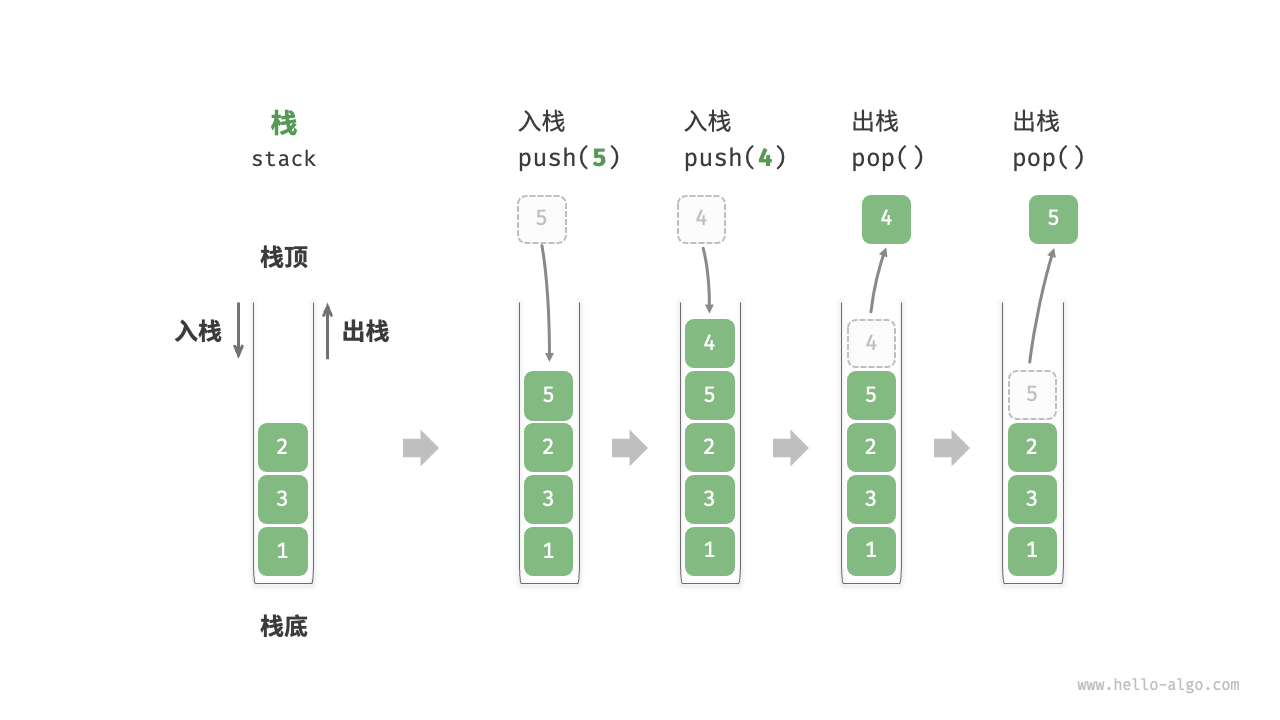
栈（Stack）是一种特殊的线性表，在这种线性表中，插入和删除运算限制在表的某一端进行。进行插入和删除 的一段叫栈顶，另一端称为栈底。

栈的最重要的性质是**后进先出(Last in, first out LIFO)**，即位于栈顶的元素相当于叠叠乐中最上面的人，最后入栈但最后出栈。

栈的基本计算如下：

• 创建一个栈
• 进栈 push()
• 出栈 pop()
• 读取栈顶元素但不弹出 top()
• 判断栈空 isEmpty()

Implementation

首先实现栈的抽象类：

由于线性表的抽象类设置了许多纯虚函数，并且栈的许多操作实现和一般的线性表差异较大。因此此处无法直接继承线性表的抽象基类。

template <typename ElementType>
class Stack
{
public:
    virtual ~Stack() {}
    virtual bool empty() const = 0;
    virtual void push(const ElementType& element) = 0;
    virtual ElementType pop() = 0;
    virtual ElementType top() const = 0;
    virtual void clear() = 0;
    //同样设置为纯虚函数
};

栈的顺序实现（类似于数组）

#pragma once
#include <iostream>
#include "Exception.h"
#include "Stack.h"

template <typename ElementType>
class SequentialStack : public Stack<ElementType>
{
private:
    ElementType* elementData;
    //存储栈元素的数组名
    int topPosition, totalCapacity;
    //栈顶序列和总容量
    void expand();

public:
    SequentialStack(int size = 10);
    ~SequentialStack();
    bool empty() const;
    void push(const ElementType& element);
    ElementType pop();
    ElementType top() const;
    void clear();
};

template <typename ElementType>
void SequentialStack<ElementType>::expand()
    //私有成员函数
{
    ElementType* TempData = elementData;
    totalCapacity *= 2;//将栈的容量扩大两倍
    elementData = new ElementType[totalCapacity];
    for (int i = 0; i <= topPosition; i++)
        elementData[i] = TempData[i];
    delete[] TempData;
}

template <typename ElementType>
SequentialStack<ElementType>::SequentialStack(int size)//构造函数
{
    elementData = new ElementType[size];
    totalCapacity = size;
    topPosition = -1;
}

template <typename ElementType>
SequentialStack<ElementType>::~SequentialStack()//destructor
{
    delete[] elementData;
}

template <typename ElementType>
bool SequentialStack<ElementType>::empty() const
{
    return topPosition == -1;
    //清空栈顶，将栈顶序列设置为特殊的-1
}

template <typename ElementType>
void SequentialStack<ElementType>::push(const ElementType& element)
{
    if (topPosition == totalCapacity - 1)
        expand();
    //说明已经存储不下了
    elementData[++topPosition] = element;
}

template <typename ElementType>
ElementType SequentialStack<ElementType>::pop()
{
    if (topPosition == -1)
        throw EmptyContainer("Error: Stack is already empty");
    return elementData[topPosition--];
}

template <typename ElementType>
ElementType SequentialStack<ElementType>::top() const
{
    if (topPosition == -1)
        throw EmptyContainer("Error: Stack is already empty");
    return elementData[topPosition];
}

template <typename ElementType>
void SequentialStack<ElementType>::clear()
{
    topPosition = -1;
}

topPosition代表栈当前的栈顶序列，如果现在栈有3个元素，这栈顶序列为2。空栈的栈顶序列为-1。

顺序栈的运算复杂度非常低：除了进栈操作需要扩充的特殊情况（即调用expand()函数），其余运算的时间复杂度均为O(1)。

栈的链接实现

在栈的链接实现中，栈顶元素就相当于是头结点。

#pragma once
#include <iostream>
#include "Exception.h"
#include "Stack.h"

template <typename ElementType>
class LinkedStack : public Stack<ElementType>
{
private:
    struct StackNode
        //和链表一样定义节点
    {
        ElementType data;
        StackNode* next;
        StackNode() : next(nullptr) {}
        StackNode(const ElementType& _data, StackNode* _next = nullptr) : data(_data), next(_next) {}
        ~StackNode() {}
    };
    StackNode* head;
    //需要维护一个指针始终指向头结点

public:
    LinkedStack();
    ~LinkedStack();
    bool empty() const;
    void push(const ElementType& element);
    ElementType pop();
    ElementType top() const;
    void clear();
};

template <typename ElementType>
LinkedStack<ElementType>::LinkedStack()
{
    head = nullptr;
}

template <typename ElementType>
LinkedStack<ElementType>::~LinkedStack()
{
    clear();
}

template <typename ElementType>
bool LinkedStack<ElementType>::empty() const
{
    return head == nullptr;
}

template <typename ElementType>
void LinkedStack<ElementType>::push(const ElementType& element)
{
    head = new StackNode(element, head);
    //从右向左读，使用构造函数创建了一个临时变量，值为element，指向的节点是当前head的地址。
    //现在将它对head进行赋值，则head指向的地址发生改变(指向现在新的栈顶元素)，而原来的栈顶元素变成了head->next所指向的
}

template <typename ElementType>
ElementType LinkedStack<ElementType>::pop()
{
    if (head == nullptr)
        throw EmptyContainer("Error: Stack is already empty");
    StackNode* temp = head;
    ElementType value = temp->data;
    head = head->next;
    //此时head指向的下一个节点成为新的栈顶元素
    delete temp;
    return value;
}

template <typename ElementType>
ElementType LinkedStack<ElementType>::top() const
{
    if (head == nullptr)
        throw EmptyContainer("Error: Stack is already empty");
    return head->data;
}

template <typename ElementType>
void LinkedStack<ElementType>::clear()
{
    StackNode* temp;
    while (head != nullptr)
    {
        temp = head;
        head = head->next;
        delete temp;
    }
}

栈的链接实现在效率上优于栈的顺序实现，因为不用扩容，不用维护topPosition。

Stack in STL

STL中的栈有四个基本运算：

• push（进栈）
• pop（出栈）
• top（返回首元素）
• empty（检查栈是否为空）

以下是一个实例代码，展示了栈的若干基本操作：

#include <iostream>
#include <stack>

int main() {
    // 创建一个整数栈
    std::stack<int> s;

    // 压入元素
    s.push(10);
    s.push(20);
    s.push(30);

    // 获取栈顶元素
    std::cout << "栈顶元素: " << s.top() << std::endl;  // 输出 30

    // 弹出栈顶元素
    s.pop();
    std::cout << "弹出后栈顶元素: " << s.top() << std::endl;  // 输出 20

    // 栈是否为空
    if (!s.empty()) {
        std::cout << "栈不为空，元素个数: " << s.size() << std::endl;  // 输出 2
    }

    return 0;
}

stack 默认使用 deque 作为底层容器，但也可以通过模板参数指定其他容器，如 vector 或 list。

std::stack<int, std::vector<int>> s;  // 使用 vector 作为底层容器
std::stack<int, std::list<int>> s;    // 使用 list 作为底层容器（链接栈的实现）

deque（双端队列）是 C++ 标准库中提供的一个容器，它可以在两端高效地插入或删除元素。它的名字 deque 是 “double-ended queue” 的缩写，表示它支持在队列的两端进行操作。我们在下一讲介绍队列的时候会详细介绍deque的用法。

Application

Recursive cleaning

Recursion

我们常常使用递归（函数嵌套函数）的方法解决问题，但是，递归会消耗大量的时间和空间复杂度。为什么？下面我们先来详细地从内存视角解释一下递归的产生机理。

在内存管理中，所谓的“栈”内存（stack memory）就是栈的操作模式相似，按照一定的规则进行分配和回收。栈内存（stack memory）主要用于存储局部变量、函数参数、函数调用的返回地址等数据。它的分配和回收非常迅速，通常是由操作系统自动管理的。栈内存的特点如下：

• 后进先出（LIFO）：栈内存的分配和回收遵循“后进先出”的规则，最近压入栈的数据会最先被弹出，这与栈数据结构的操作模式一致。
• 自动管理：栈内存的分配和释放由系统自动管理，通常是函数的调用和返回过程中，栈帧（stack frame）的创建和销毁。
• 空间有限：栈的大小通常是固定的，超过限制时会发生栈溢出（stack overflow）。

我们先来看一种比较特殊的情况，函数的嵌套调用。在main函数中，函数调用max函数，在max函数中，函数调用p函数，形成了函数调用的一种三层嵌套。上文讲过，函数体内部的局部变量通常是存储在栈内存上的。这些局部变量在函数调用时被创建，并在函数返回时自动销毁（具体的过程如上图右侧所演示）。也就是说，当函数嵌套的层数变多时，系统执行这一个过程所需的最大栈内存会不断递增。

回到递归的例子，当递归层数增多时，在栈内存上的栈帧空间会不断变大（因为上一级的函数没有返回对应的值，函数的调用没有结束，所有栈内存上会一直保留着函数的上下文）。这会带来极大的内存消耗！！！

目前一些编译器对尾递归优化可以不保留上下文，但是对于没有尾递归的情况（例如回溯算法），则栈内存的低效使用是递归不得不面对的问题。

Using Stack instead of Recursion

下面看一个程序实例：我们需要打印正整数的值：

没事找事做的程序（乐）

如果使用递归函数：

#include <iostream>
using namespace std;
void print(int num){
    if(num<10){
        cout<<num;
    }else{
        print(num/10);  //Recursion
        cout<<num%10;
    }
}
int main(){
    int N;cin>>N;
    print(N);
    return 0;
}

这个递归实现本身较为简单，但是当递归深度较大时，该算法对栈内存的利用率非常低，例如，系统会在栈内存上分配栈帧，即为每一层函数存储局部变量、函数参数、返回地址等信息。但是，我们只希望存储一个值！

因此，我们可以从内存的视角优化递归算法。使用栈消除递归就是程序员自己模拟函数的调用，自己维护一个栈来存储目标值。

#include <iostream>
#include <stack>
using namespace std;
void print(long long num){
    stack<int> s;
    int tmp;
    int maxsize=0;
    s.push(num);
    maxsize++;
    while(!s.empty()){
        if(s.top()>9){
            tmp=s.top();
            s.pop();
            s.push(tmp%10);
            s.push(tmp/10);
            maxsize=max(maxsize,int(s.size()));
        }else{
            cout<<s.top();
            s.pop();
        }
    }
    cout<<endl<<"The maxsize of the stack: "<<maxsize<<endl;
}
int main(){
    long long N;cin>>N;
    print(N);
    return 0;
}

1234567
1234567
The maxsize of the stack: 7

从内存视角来比较两者的差异：

#include <iostream>
using namespace std;
void print(int num){
    cout<<&num<<endl;
    if(num<10){
        cout<<num;
    }else{
        print(num/10);
        cout<<num%10;
    }
}
int main(){
    int N;cin>>N;
    print(N);
    return 0;
}

1234567
0x61fdf0
0x61fdc0
0x61fd90
0x61fd60
0x61fd30
0x61fd00
0x61fcd0
1234567

可以看出，函数的递归深度为7，自定义的栈的内存最大值也为7。但是在函数调用时，仅函数调用就用了288bytes，而栈的内存仅仅只是224bytes。（估算）

虽然相差只是几个字节的差距，但是一旦递归深度变大且数据类型本身所占内存数变多，这个开销将会大大的增长。

括号配对

在敲代码的过程中，相信大家都会遇到过括号太多或者括号不匹配的情况。编译器需要检查括号匹配的情况，并在发现异常时及时地报错。但是，括号具有多种类型：()``[]``{}，并且有些相互匹配的括号之间的间隔非常遥远。我们能够仅在一次扫描的过程中完成对括号配对的检查？

下面为了方便，我们将([{称为开括号，将)]}称为闭括号。

这个问题使用栈，可以很高效地解决。基本思路是：遇到闭括号时，将与最近遇到的且尚未被匹配的开括号进行匹配。

“最近遇到的的括号”和栈的LIFO特性不谋而合！

确定基本算法的思想后，我们来细分到每一个步骤的实现：

• 创建一个栈来维护括号的存储。（更具体来说：维护开括号的存储）
• 如果读取到一个开括号，进栈。
  • 因为匹配工作是依据闭括号来进行的，所以开括号进栈的时候不需要额外的操作。
• 如果读取到一个闭括号，则与栈顶的开括号进行匹配。（位于栈顶的开括号就是最近遇到的且尚未被匹配的开括号）
  • 如果匹配成功，那么这一对括号匹配成功，将开括号弹出栈。
  • 如果匹配失败，说明无法匹配。（例如[{(}])，直接return false。
  • 如果此时栈已空，则说明不匹配。（闭括号的数量多于开括号的数量）
• 完成所有的扫描后，若栈非空，则说明开括号的数量多于闭括号的数量。匹配失败。

#include <iostream>
#include <stack>
using namespace std;
bool judgethemarkers(string s){
    stack<char> themarker;
    for(auto ch:s){
        if(ch=='('||ch=='['||ch=='{'){
            themarker.push(ch);
        }else{
            if(themarker.empty()) return false;
            char check=themarker.top();
            if(ch==']'&&check=='[') themarker.pop();
            else if(ch==')'&&check=='(') themarker.pop();
            else if(ch=='}'&&check=='{') themarker.pop();
            else return false;
        }
    }
    if(!themarker.empty()) return false;
    return true;
}
int main(){
    string s;
    cin>>s;
    cout<<(judgethemarkers(s)?"Successful":"Unsuccessful");
    return 0;
}

至此，栈的扫描功能已经完全实现，但是还有很多细节需要被优化：

• 当括号出现在字符串，字符常量，注释中时，我们不希望括号被统计。
• 实现更高级的功能，例如定位到具体哪个位置的括号匹配出现问题。

为此，我们实现一个更加复杂的balance类，作为一个检查文件中代码括号匹配的工具。

#include <fstream>  // for file input handling
using namespace std;

class balance
{
private:
    ifstream fin;      // File stream to be checked
    int currentLine;   // Current line being processed
    int Errors;        // Count of errors found

    // Structure representing a symbol and its line number
    struct Symbol {
        char Token;     // Character token (e.g., braces, parentheses)
        int TheLine;    // Line number where the token is found
    };

    // Enum for comment types
    enum CommentType {
        SlashSlash,     // C++ style comment (//)
        SlashStar       // C style comment (/* */)
    };

    // Utility functions for CheckBalance
    bool CheckMatch(char Symb1, char Symb2, int Line1, int Line2); // Check if two symbols match (e.g., '(' and ')')
    char GetNextSymbol();          // Get the next valid symbol from the input
    void PutBackChar(char ch);     // Push back a character to the input stream
    void SkipComment(enum CommentType type); // Skip over comments (C or C++ style)
    void SkipQuote(char type);     // Skip over quoted strings or characters
    char NextChar();               // Get the next character from the input file

public:
    // Constructor: Opens the file for checking
    balance(const char *s);

    // Check if the brackets/parentheses in the file are balanced
    int CheckBalance();
    class noFile{};//for the exception
};

除了构造函数之外，公有函数只有CheckBalance，其他工具函数全部为私有函数的形式，用户不需要直接调用。（对用户而言只提供唯一的接口，对程序员而言将不同的子功能在内部封装。）

具体功能的实现比较复杂，敬请期待后续的更新~

简单的计算器

中缀表达式：算术表达式总是出现在两个操作数之间。例如5*(7-2*3)+8/2。

我们似乎总是能够一样看出中缀表达式的运算结果，真的吗？

不妨来看下面的中缀表达式：( ( ( 3 + 5 * ( 2 - 8 ) ) / ( sin(45) + 2^3 ) ) * ( log(100, 10) - sqrt(16) ) + max(1, 2, 3) % 4 ) ^ 2 + abs( -10 ) * factorial(3) - ( min(5, 10, 15) + ceil(4.3) ) / floor(2.9)。

这个时候或许就有点吃力了，为什么？因为中缀表达式的运算优先级往往并不总是从左向右：

• 有时候我们需要提前运算括号里面的内容
• 没有括号是不同的运算符也有不同的运算优先级。

对于计算机而言，这个任务或许更加的艰巨——计算机无法识别输入顺序和计算顺序之间的差别。

于是，我们希望改写中缀表达式，并将其转化为后缀表达式（逆波兰表达式），后缀表达式将运算符放在运算数之后，并且运算顺序和阅读顺序保持一致。

例如，中缀表达式5*(7-2*3)+8/2转化为后缀表达式为5 7 2 3 * - * 8 2 / +，计算机在阅读后缀表达式时，只需要从左往右不断输入，遇到运算符，则取之前的两个运算数做乘法，并将运算结果代替该子表达式。

对于上面的例子，后缀表达式的运算结果如下：

步骤 1：初始化

• 栈：[]
• 输入：5 7 2 3 * - * 8 2 / +

步骤 2：处理数字 5

• 将 5 压入栈。
• 栈：[5]
• 输入：7 2 3 * - * 8 2 / +

步骤 3：处理数字 7

• 将 7 压入栈。
• 栈：[5, 7]
• 输入：2 3 * - * 8 2 / +

步骤 4：处理数字 2

• 将 2 压入栈。
• 栈：[5, 7, 2]
• 输入：3 * - * 8 2 / +

步骤 5：处理数字 3

• 将 3 压入栈。
• 栈：[5, 7, 2, 3]
• 输入：* - * 8 2 / +

步骤 6：处理运算符 *

• 弹出栈顶的两个数字：3 和 2。
• 计算：2 * 3 = 6。
• 将结果 6 压入栈。
• 栈：[5, 7, 6]
• 输入：- * 8 2 / +

步骤 7：处理运算符 -

• 弹出栈顶的两个数字：6 和 7。
• 计算：7 - 6 = 1。
• 将结果 1 压入栈。
• 栈：[5, 1]
• 输入：* 8 2 / +

步骤 8：处理运算符 *

• 弹出栈顶的两个数字：1 和 5。
• 计算：5 * 1 = 5。
• 将结果 5 压入栈。
• 栈：[5]
• 输入：8 2 / +

步骤 9：处理数字 8

• 将 8 压入栈。
• 栈：[5, 8]
• 输入：2 / +

步骤 10：处理数字 2

• 将 2 压入栈。
• 栈：[5, 8, 2]
• 输入：/ +

步骤 11：处理运算符 /

• 弹出栈顶的两个数字：2 和 8。
• 计算：8 / 2 = 4。
• 将结果 4 压入栈。
• 栈：[5, 4]
• 输入：+

步骤 12：处理运算符 +

• 弹出栈顶的两个数字：4 和 5。
• 计算：5 + 4 = 9。
• 将结果 9 压入栈。
• 栈：[9]
• 输入：（空）

到这里，我们已经找到了实现简单计算器的基本思路：

• 等待用户输入一个字符串（中缀表达式），并检查合法性。
• 将中缀表达式转化为后缀表达式。
• 对后缀表达式处理，得到最终的运算结果。

如何实现中缀转后缀？在这里比较示例中的中缀表达式和后缀表达式：中缀表达式5*(7-2*3)+8/2转化为后缀表达式为5 7 2 3 * - * 8 2 / +，我们发现：

• 对于运算数而言，运算数之间的顺序保持不变
• 运算符之间的相对位置发生了变化
  • 如何改变？依据运算符的优先级

在这里我们只实现四种运算：加减、乘除、乘方、括号，其优先级递增。对于相同优先级的情况，加减和乘除运算符合左结合规律，乘方优先级符合右结合规律。根据这个规律， 我们来分析5*(7-2*3)+8/2的运算过程。首先进行的运算是2*3，因此后缀表达式中一定有一个部分是2 3 *,接下来执行运算7-6,其中6是第一步运算生成的操作数，因此这一部分可以被扩写为7 2 3 * -，以此类推，可以写出最后的后缀表达式。

总结规律，我们发现，我们总是先人为地找到中缀表达式的优先运算的部分，然后不断在字符串的两端扩写后缀表达式。关键的部分，我们应该如何让计算机确定哪个部分是优先运算的部分？

为了解决这个问题，我们不妨模拟计算机，计算机会按照顺序读入表达式的运算数和运算符，如果读入运算数，就在输出的字符串后直接添加。（因为运算数不会改变运算顺序，运算符才是重点！）如果读入运算符，我们需要维护一个栈来控制进出顺序。

使用栈的核心原因是控制运算符输入顺序和输出顺序不同。

在读入运算符的时候，因为不确定其是否能直接做运算（5*(7-2*3)+8/2读到减号后，无法确定是否要执行7-2，因为2的右边还有一个未知的运算符，无法确定优先级），因此运算符需要进栈。

如何确定运算符的出栈顺序？一条普适规律：如果存在栈内运算符的优先级高于或等于新进栈的运算符的优先级（乘方右结合除外），那么说明这些运算符会先于这个新进栈的运算符被运算，因此需要按顺序全部出栈。

出栈顺序就代表着运算符的实际被运算顺序！

对于括号而言，由于括号并不会出现在后缀表达式中，因此，括号只是起到了一个隔离的作用，相当于开闭括号之间是一个小的表达式。

综上所述，我们可以归纳中缀转后缀的运算法则：

• 运算数：立即输出
• 开括号：进栈
• 闭括号：不进栈，同时不断清栈直到遇到第一个开括号，把这个开括号出栈
• 乘方：进栈（乘方运算是右结合，且运算的优先级最高，所以读入乘方肯定无法确定是否要运算，且栈内也不会有运算符的优先级高于乘方）
• 乘除：进栈且退栈直到遇到加，减或左括号
• 加减：先进栈，再退栈直到栈为空或遇到左括号
• 读入结束后清栈

这就是中缀转后缀的基本操作，后续的实现就很简单了：按顺序扫描后缀表达式（后缀表达式本质上也用一个栈来维护）至此，我们便完成了简单计算器的算法原理的构思。

不过这还没有完，因为使用的都是栈，因此这两步本质上可以进行合并，即维护运算数栈和运算符栈，在实现中缀转后缀的过程中，一旦运算符栈弹出一个运算符，运算数栈立刻弹出两个运算数，并且将运算后的运算数重新入栈。

接下来就是漫长的Coding过程，以下是实现简单计算器功能的Cauculate类：

#include <iostream>
#include <cstring>
#include <stack>
#include <cctype>
#include <algorithm>
#include <sstream>
#include <cmath>
using namespace std;

class Calculate {
private:
    string expression;  // 存储用户输入的表达式
    bool check_if_available();  // 检查表达式是否合法
public:
    Calculate(string input_ = "No input") : expression(input_) {
        // 删除空白字符
        expression.erase(std::remove_if(expression.begin(), expression.end(), ::isspace), expression.end());
    }
    double calculate_result();  // 计算表达式的结果
};

// 检查字符是否是运算符
inline bool check_op(char ch) {
    return ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^';
}

// 检查字符是否是括号
inline bool check_Parentheses(char ch) {
    return ch == '(' || ch == ')';
}

// 根据运算符计算两个操作数的结果
double cal(char op, double a, double b) {
    switch (op) {
        case '+': return a + b;
        case '-': return a - b;
        case '*': return a * b;
        case '/': return a / b;
        case '^': return pow(a, b);
        default: return 0;  // 默认返回 0
    }
}

// 执行栈操作：弹出运算符和操作数，计算结果并压入栈中
void Stack_operation(stack<double>& numstack, stack<char>& opstack) {
    char op = opstack.top();  // 弹出栈顶运算符
    opstack.pop();
    double num1 = numstack.top(); numstack.pop();  // 弹出第一个操作数
    double num2 = numstack.top(); numstack.pop();  // 弹出第二个操作数
    numstack.push(cal(op, num2, num1));  // 计算结果并压入栈中
}

// 检查表达式是否合法
bool Calculate::check_if_available() {
    if (expression == "No input") {
        cout << "Please input a string!" << endl;
        return false;
    }

    int size = expression.length();
    stack<char> parentheses;  // 用于检查括号匹配

    for (int i = 0; i < size; i++) {
        char ch = expression[i];

        // 检查括号
        if (check_Parentheses(ch)) {
            if (ch == '(') {
                parentheses.push('(');  // 左括号入栈
            } else {
                if (parentheses.empty() || parentheses.top() != '(') {
                    cout << "Parentheses match fault!" << endl;
                    return false;
                }
                parentheses.pop();  // 右括号匹配成功，弹出左括号
            }
        }

        // 检查运算符
        else if (check_op(ch)) {
            if (i == 0 || i == size - 1) {
                cout << "Operation Error!" << endl;
                return false;
            }

            char prev = expression[i - 1];  // 运算符前一个字符
            char next = expression[i + 1];  // 运算符后一个字符
            if (!((isdigit(prev) || prev == ')') && (isdigit(next) || next == '('))) {
                cout << "Operation Error!" << endl;
                return false;
            }
        }

        // 检查非法字符
        else if (!isdigit(ch) && ch != '.') {
            cout << "INVALID LETTERS" << endl;
            return false;
        }
    }

    // 检查括号是否全部匹配
    if (!parentheses.empty()) {
        cout << "Parentheses match fault!" << endl;
        return false;
    }

    return true;
}

// 计算表达式的结果
double Calculate::calculate_result() {
    if (!this->check_if_available()) {
        cout << "Wrong!" << endl;
        exit(1);
    }

    stack<char> opstack;  // 运算符栈
    stack<double> numstack;  // 操作数栈
    int size = expression.length();

    for (int i = 0; i < size; i++) {
        char ch = expression[i];

        // 处理数字和小数点
        if (isdigit(ch) || ch == '.') {
            stringstream ss;
            while (i < size && (isdigit(expression[i]) || expression[i] == '.')) {
                ss << expression[i++];  // 将数字和小数点拼接到字符串流中
            }
            i--;  // 回退一步，因为外层循环会再增加一次 i
            double num;
            ss >> num;  // 将字符串流转换为浮点数
            numstack.push(num);  // 将数字压入操作数栈
        }

        // 处理运算符和括号
        else {
            switch (ch) {
                case '(':
                    opstack.push(ch);  // 左括号直接入栈
                    break;

                case ')':
                    // 弹出栈顶运算符并计算，直到遇到左括号
                    while (!opstack.empty() && opstack.top() != '(') {
                        Stack_operation(numstack, opstack);
                    }
                    if (!opstack.empty() && opstack.top() == '(') {
                        opstack.pop();  // 弹出左括号
                    } else {
                        cout << "Parentheses match fault!" << endl;
                        exit(1);
                    }
                    break;

                case '^':
                    // 乘方运算符优先级最高，直接入栈
                    opstack.push(ch);
                    break;

                case '*':
                case '/':
                    // 处理乘法和除法运算符
                    while (!opstack.empty() && opstack.top() != '(' &&
                        (opstack.top() == '^' || opstack.top() == '*' || opstack.top() == '/')) {
                        Stack_operation(numstack, opstack);
                    }
                    opstack.push(ch);  // 当前运算符入栈
                    break;

                case '+':
                case '-':
                    // 处理加法和减法运算符
                    while (!opstack.empty() && opstack.top() != '(' &&
                        (opstack.top() == '^' || opstack.top() == '*' || opstack.top() == '/' ||
                            opstack.top() == '+' || opstack.top() == '-')) {
                        Stack_operation(numstack, opstack);
                    }
                    opstack.push(ch);  // 当前运算符入栈
                    break;

                default:
                    // 非法字符（已经在 check_if_available 中检查过，这里不会执行）
                    break;
            }
        }
    }

    // 清空栈中剩余的运算符
    while (!opstack.empty()) {
        Stack_operation(numstack, opstack);
    }

    // 返回最终结果
    return numstack.top();
}

int main() {
    string inputstr;
    while (true) {
        cout << "Enter the expression (or 'q' to quit): " << endl;
        getline(cin, inputstr);
        if (inputstr == "q") break;
        Calculate test(inputstr);
        cout << "Result: " << test.calculate_result() << endl;
    }
    return 0;
}