DataStructure Splay Tree

伸展树

平衡树的缺陷

• 实现复杂
• 90-10规则：如果百分之九十的访问数据都是针对百分之10的数据，平衡查找树在这里毫无优势。（平衡树保证了最差的实现复杂度的情况仍然是$O(\log n)$的）

在很多的应用场景下，我们不需要考虑极端的最坏时间复杂度情形，而应该关注均摊时间复杂度，也就是说，我们希望在访问中不断重构这棵树，使更经常被访问的数据朝着根移动，我们把这样的过程称为向根旋转。

伸展树的基础仍然是二叉查找树！因此在旋转的过程中需要保证有序性。（不改变中序遍历的顺序）

这种思路和哈夫曼树和哈夫曼编码如出一辙。

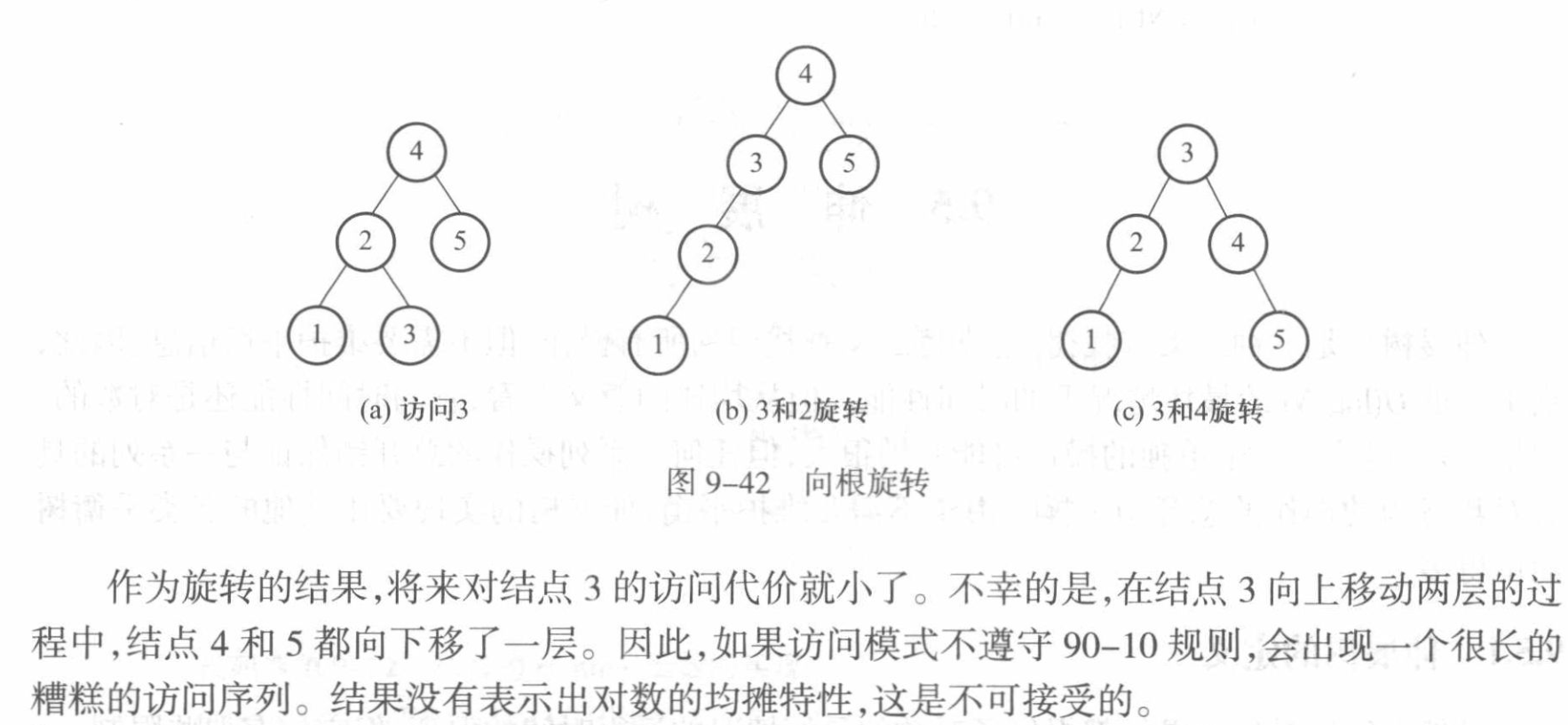
不过这会带来一个严重的问题：每一次被访问元素离根更近，但是一定存在元素离根更远，这样无法实现均摊的时间复杂度！并且只使用单旋转会产生一些非常深的节点（$O(N)$），因此，我们需要双旋转和伸展操作来实现均摊的对数时间复杂度。

注意，伸展树需要保证90-10操作，如果对每一个元素都进行访问，那最后会退化到$O(N)$的时间复杂度。

伸展操作

我们记$X$为要旋转的路径上的非根节点。

• X的父节点是根
• X是祖父节点的内部节点
• X是祖父节点的外部节点

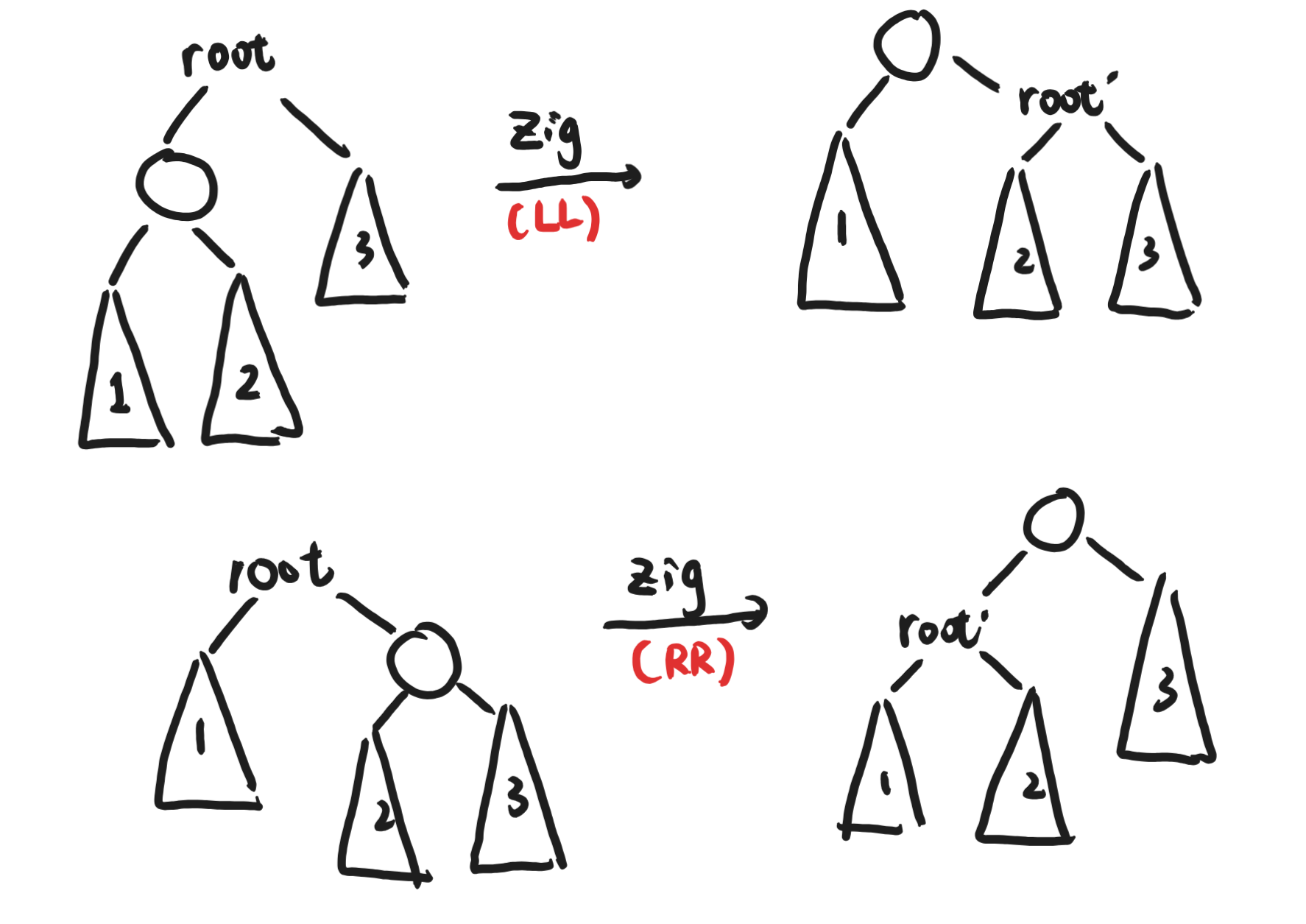
zig

采用一个单旋转，将$X$旋转到根，完全类似于AVL树的LL旋转和RR旋转。

zig-zag

对于第二种情况，如果值使用单旋转很容易产生退化的情况，因此需要进行双旋转（完全类似于AVL树中的RL或者LR旋转）。

“Zigzag” 是一个英语词汇，字面意思是“锯齿形”或“之字形”。它通常用于描述一种折线或曲线的形状，表现出交替的向上和向下的运动。

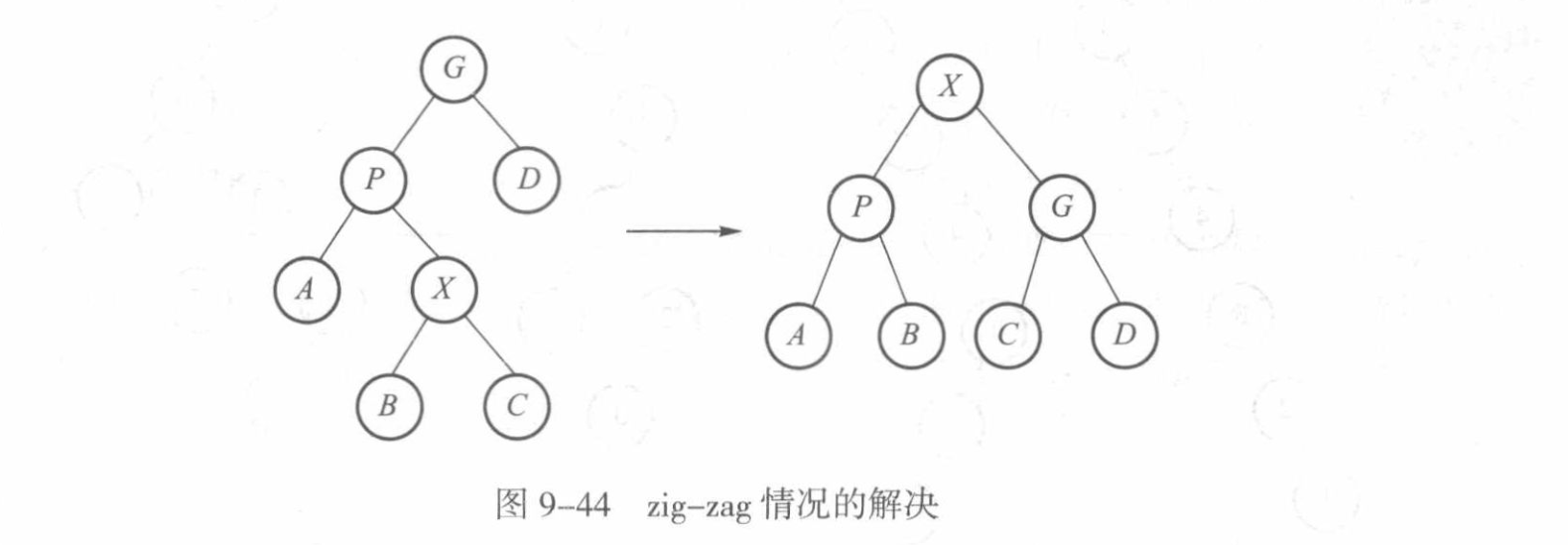
例如这里目标节点是$X$，如果只进行一次zig操作，会导致树的左侧不断倾斜（画一下图就知道了），因此需要模拟AVL树中的双旋转操作来维护平衡性。（降低了树的整体高度）

奇思妙想：伸展树是不是就是哈夫曼编码和AVL树的结合呢？

zig-zig

对于外侧节点，同样需要两次zig操作。看下面的图例：

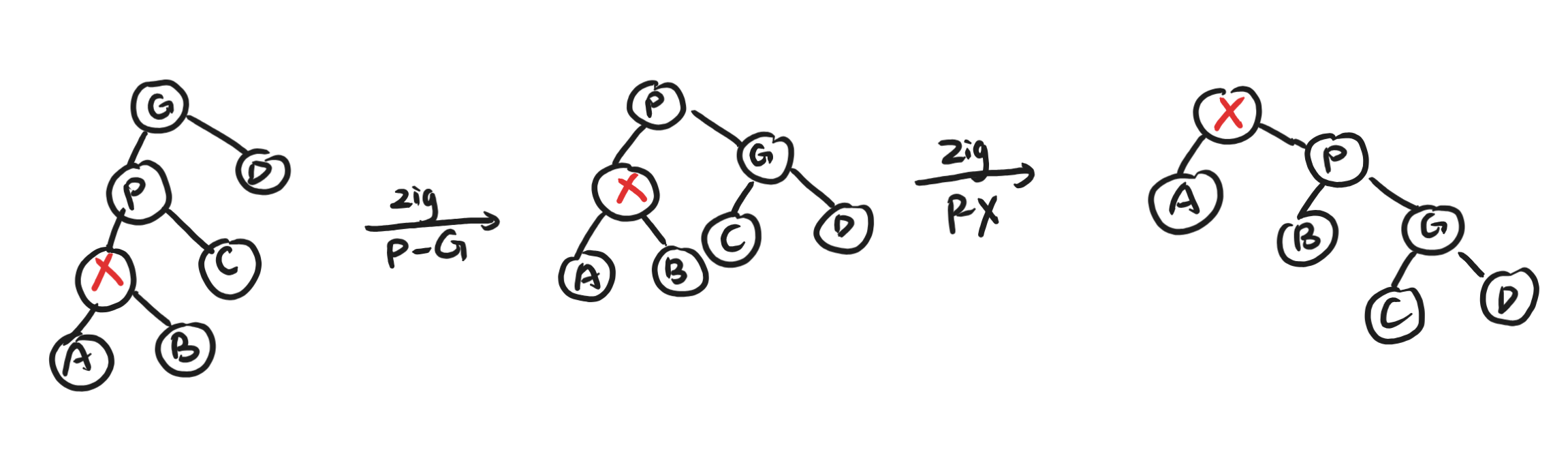
在这里树的高度没有发生变化，但是$X$成功离根节点更近了。

插入和删除

伸展树的插入和删除操作几乎和二叉查找树一模一样，就是多了一步将被访问节点伸展到根节点的过程。

因此算法的基本思路：

• 最基本的子操作：伸展splay(root, key)
  • 查找以root为根的子树中是否存在元素的键值为key，如果有，那么通过伸展操作将其上提到根节点。
    • 严格意义上来说，splay 操作会将最近访问的节点（无论是存在的节点还是最接近的节点）提升到根节点。如果最后访问的节点就是目标节点，那当然是这样。
  • 其还有一个附加的作用：如果key不存在，意味着其将搜索到叶节点，而叶节点会变成当前的根节点！也就是说此时树会变的非常倾斜。（即现在root的一个孩子节点是空的）
• 插入操作：
  • 首先做伸展操作（附带着查找）
    • 如果找到了，那么此时对应节点肯定位于根节点，修改对应的值即可。
    • 如果没有找到，此时树的一侧节点被置空（具体是哪一侧和进行的伸展操作有关），接上去就可以了
  • 然后创建新节点，链接节点并且更新根节点。
• 删除操作：
  • 首先伸展+查找
    • 如果没有找到（直接返回）
    • 如果找到了并且键值相同，删除节点 & 构建新的子树
      • 如果左节点为空，直接把右子树当做新的树。
      • 如果不为空，那么对左子树再splay一次，此时肯定可以保证找不到，因此腾出一个孩子给原先根节点的右子树（并且可以保证有序性）。

代码实现

#include <iostream>

template<typename Key, typename Value>
class SplayTree {
private:
    struct Node {
        Key key;
        Value value;
        Node *left;
        Node *right;

        Node(Key k, Value v) : key(k), value(v), left(nullptr), right(nullptr) {}
    };

    Node *root;

    // Right rotation
    Node *rotateRight(Node *node) {
        Node *newRoot = node->left;
        node->left = newRoot->right;
        newRoot->right = node;
        return newRoot;
    }

    // Left rotation
    Node *rotateLeft(Node *node) {
        Node *newRoot = node->right;
        node->right = newRoot->left;
        newRoot->left = node;
        return newRoot;
    }

    /**
     * @brief splay the node to the root node with the value key
     * 
     * @param node the original root node
     * @param key the value to be splayed to the root node
     * @return Node* 
     */
    Node *splay(Node *node, Key key) {
        if (!node || node->key == key) {
            return node;
        }

        // Key lies in the left subtree
        if (key < node->key) {
            if (!node->left) return node;

            // Zig-Zig (Left Left)
            if (key < node->left->key) {
                node->left->left = splay(node->left->left, key);
                node = rotateRight(node);
            }
            // Zig-Zag (Left Right)
            else if (key > node->left->key) {
                node->left->right = splay(node->left->right, key);
                if (node->left->right) {
                    node->left = rotateLeft(node->left);
                }
            }

            return node->left ? rotateRight(node) : node;
        }
        // Key lies in the right subtree
        else {
            if (!node->right) return node;

            // Zag-Zig (Right Left)
            if (key < node->right->key) {
                node->right->left = splay(node->right->left, key);
                if (node->right->left) {
                    node->right = rotateRight(node->right);
                }
            }
            // Zag-Zag (Right Right)
            else if (key > node->right->key) {
                node->right->right = splay(node->right->right, key);
                node = rotateLeft(node);
            }

            return node->right ? rotateLeft(node) : node;
        }
    }

    // Helper function to delete a node
    Node *deleteNode(Node *node, Key key) {
        if (!node) return nullptr;

        node = splay(node, key);

        // If the key is not found, return the original tree
        if (node->key != key) return node;

        // If the key is found, delete the root node
        if (!node->left) {
            Node *temp = node->right;
            delete node;
            return temp;
        } else {
            Node *temp = node->left;
            temp = splay(temp, key);
            temp->right = node->right;
            delete node;
            return temp;
        }
    }

public:
    SplayTree() : root(nullptr) {}

    // Insert a key-value pair
    void insert(Key key, Value value) {
        if (!root) {
            root = new Node(key, value);
            return;
        }

        root = splay(root, key);

        if (root->key == key) {
            root->value = value;// Update value if key already exists
            return;
        }

        Node *newNode = new Node(key, value);
        if (key < root->key) {
            newNode->right = root;
            newNode->left = root->left;
            root->left = nullptr;
        } else {
            newNode->left = root;
            newNode->right = root->right;
            root->right = nullptr;
        }
        root = newNode;
    }

    // Find a key and return its value
    Value *find(Key key) {
        root = splay(root, key);
        if (root && root->key == key) {
            return &root->value;
        }
        return nullptr;
    }

    // Delete a key
    void remove(Key key) {
        root = deleteNode(root, key);
    }

    // Print the tree (in-order traversal)
    void print() {
        if (root == nullptr) {
            std::cout << "The Tree is empty" << std::endl;
            return;
        }
        printHelper(root);
        std::cout << std::endl;
    }

private:
    void printHelper(Node *node) {
        if (!node) return;
        printHelper(node->left);
        std::cout << "(" << node->key << ", " << node->value << ") ";
        printHelper(node->right);
    }
};

int main() {
    SplayTree<int, std::string> tree;

    // Insert elements
    std::cout << "Inserting elements into the tree:" << std::endl;
    tree.insert(10, "Ten");
    tree.insert(20, "Twenty");
    tree.insert(30, "Thirty");
    tree.insert(5, "Five");
    tree.insert(15, "Fifteen");
    tree.insert(25, "Twenty-Five");
    tree.insert(35, "Thirty-Five");
    tree.print();

    // Find elements
    std::cout << "\nFinding key 20:" << std::endl;
    auto value = tree.find(20);
    if (value) {
        std::cout << "Found: " << *value << std::endl;
    } else {
        std::cout << "Key not found." << std::endl;
    }

    std::cout << "\nFinding key 40 (non-existent):" << std::endl;
    value = tree.find(40);
    if (value) {
        std::cout << "Found: " << *value << std::endl;
    } else {
        std::cout << "Key not found." << std::endl;
    }

    // Delete elements
    std::cout << "\nDeleting key 10:" << std::endl;
    tree.remove(10);
    tree.print();

    std::cout << "\nDeleting key 30:" << std::endl;
    tree.remove(30);
    tree.print();

    std::cout << "\nDeleting key 5:" << std::endl;
    tree.remove(5);
    tree.print();

    std::cout << "\nDeleting key 40 (non-existent):" << std::endl;
    tree.remove(40);
    tree.print();

    // Edge case: Insert duplicate key
    std::cout << "\nInserting duplicate key 20 with new value 'Updated Twenty':" << std::endl;
    tree.insert(20, "Updated Twenty");
    tree.print();

    // Edge case: Insert into an empty tree
    std::cout << "\nClearing the tree and inserting into an empty tree:" << std::endl;
    tree.remove(15);
    tree.remove(25);
    tree.remove(35);
    tree.remove(20);
    tree.print();

    tree.insert(50, "Fifty");
    tree.print();

    return 0;
}

输出结果：

Inserting elements into the tree:
(25, Twenty-Five) (15, Fifteen) (5, Five) (10, Ten) (20, Twenty) (30, Thirty) (35, Thirty-Five) 

Finding key 20:
Key not found.

Finding key 40 (non-existent):
Key not found.

Deleting key 10:
(25, Twenty-Five) (15, Fifteen) (5, Five) (10, Ten) (20, Twenty) (30, Thirty) (35, Thirty-Five) 

Deleting key 30:
(25, Twenty-Five) (15, Fifteen) (5, Five) (10, Ten) (20, Twenty) (35, Thirty-Five) 

Deleting key 5:
(25, Twenty-Five) (15, Fifteen) (5, Five) (10, Ten) (20, Twenty) (35, Thirty-Five) 

Deleting key 40 (non-existent):
(25, Twenty-Five) (15, Fifteen) (5, Five) (10, Ten) (20, Twenty) (35, Thirty-Five) 

Inserting duplicate key 20 with new value 'Updated Twenty':
(25, Twenty-Five) (15, Fifteen) (5, Five) (10, Ten) (20, Updated Twenty) (35, Thirty-Five) 

Clearing the tree and inserting into an empty tree:
(15, Fifteen) (5, Five) (10, Ten) 
(15, Fifteen) (5, Five) (10, Ten) (50, Fifty)