DataStructure-RBT-Tree

Red-Black Tree

Definition

红黑树需要满足如下的平衡性：

• 每个结点被标记为红色或者黑色

• 根节点是黑色

  • 一般来说，我们也会定义nullptr为黑色，并且把这些空节点定义为“叶节点”会更有利于分析。（Due to Definition 4）

• 节点红色 -> 子节点是黑色

  • 不可以存在两个连续的红色节点

• 从任何一个节点出发到空节点（通常认为空节点为黑色节点），必须包含相同数量的黑色节点。

从红黑树的定义出发，我们可以证明：红黑树保证$O(h) = O(\log n)$.

• 如果任何一条从根节点到空节点的路径上存在$H$个黑色的节点，则整棵树必须至少有$2^H -1$个黑色节点，至多有$2^{2H} -1$个节点。
  • 证明:可以形象的理解为一颗被压缩的二叉树，即把所有的红色节点删除，并且每一个黑色节点都有2个儿子（叶子结点除外），则根据完全二叉树的性质，$n \le 2^H -1$，并且$H$同时还代表着全黑的最短路径（如果存在的话）。
  • 相反的，节点数最多的情况就是红黑节点交替排列，因此是一颗高度为$2H$的满二叉树，$n \ge 2^{2H} -1 $。，同时，这也代表着最长的路径。
• 有公式$n \ge 2^{2H} -1 $，取对数即可证明$O(h) = O(\log n)$。

Insert

将新节点插入到叶子结点，此时关键需要判断树是否满足RBT的四条基本定义。为了不破坏定义4，我们需要将插入的节点染色成红色节点。接下来：

• 如果父亲节点是黑色节点：插入过程完成。
• 如果父亲节点是红色节点：需要进行调整

下面，分成两种情况：

Case1: 父亲节点P的兄弟节点S是黑色的

如果X是P的外侧节点，则操作对应LL或者RR的情况，只需要单旋转一次即可，同时保证当前根节点仍然保证黑色，这样就不用继续调整后祖先节点，并且也调整了树的结构使其不出现染色冲突的问题。

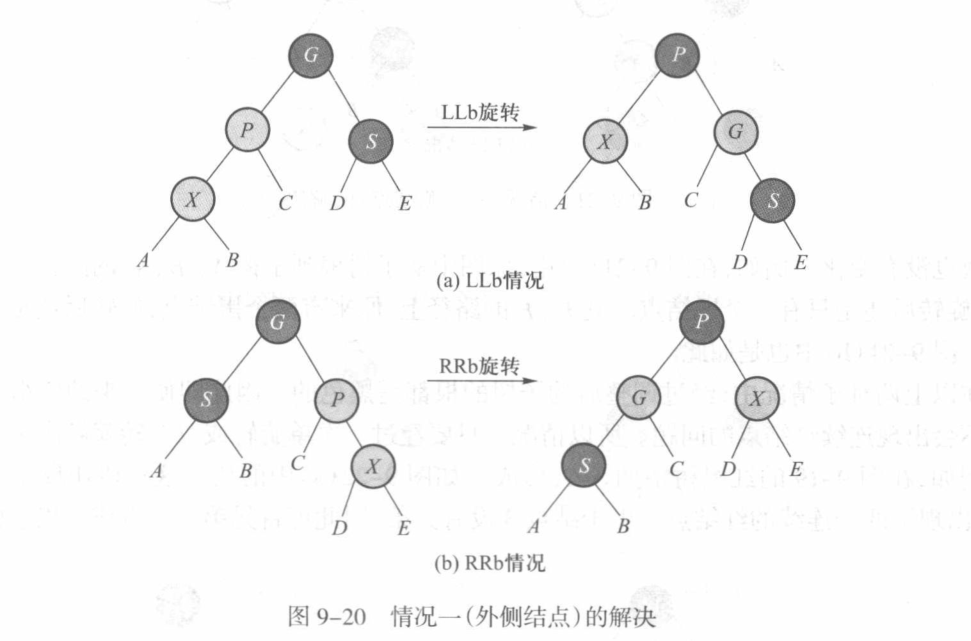
如果X是P的内侧节点，类似于RL旋转和LR旋转，实现结构的调整：

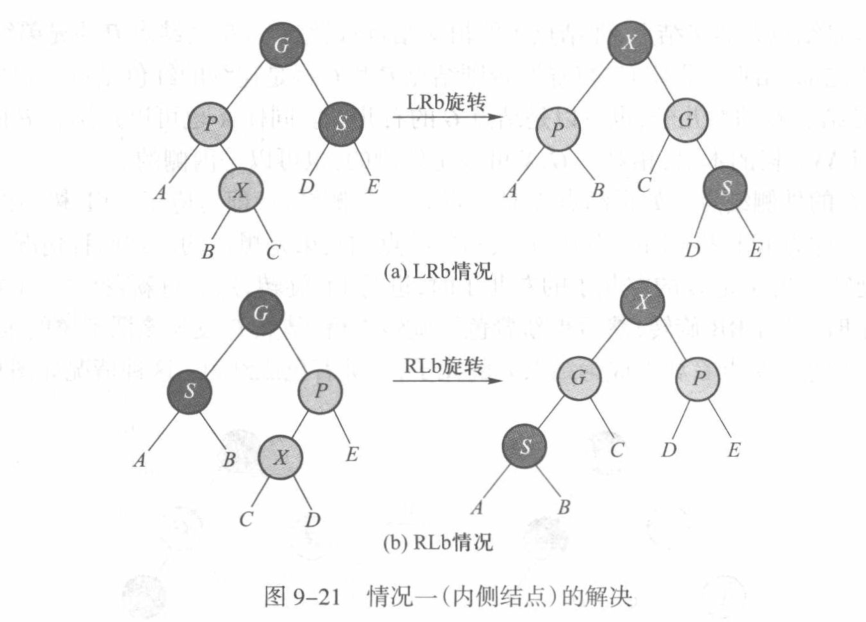
同理，也需要注意保持当前根节点依旧是黑色的。

Case2: 父亲节点P的兄弟节点S是红色的

此时祖父节点一定是黑色节点，因此只需要父亲层和祖父层的颜色交换即可，但是，此时有可能上部的结构发生了破坏，需要不断向上检查。（此时有可能会变成Case1，见下图）

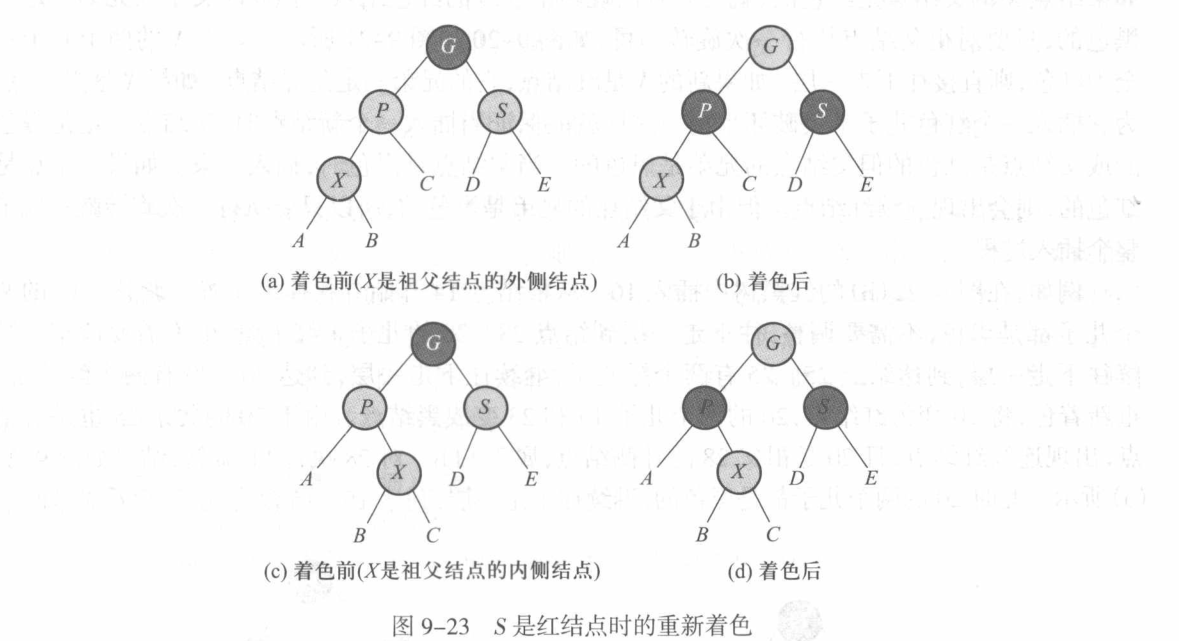
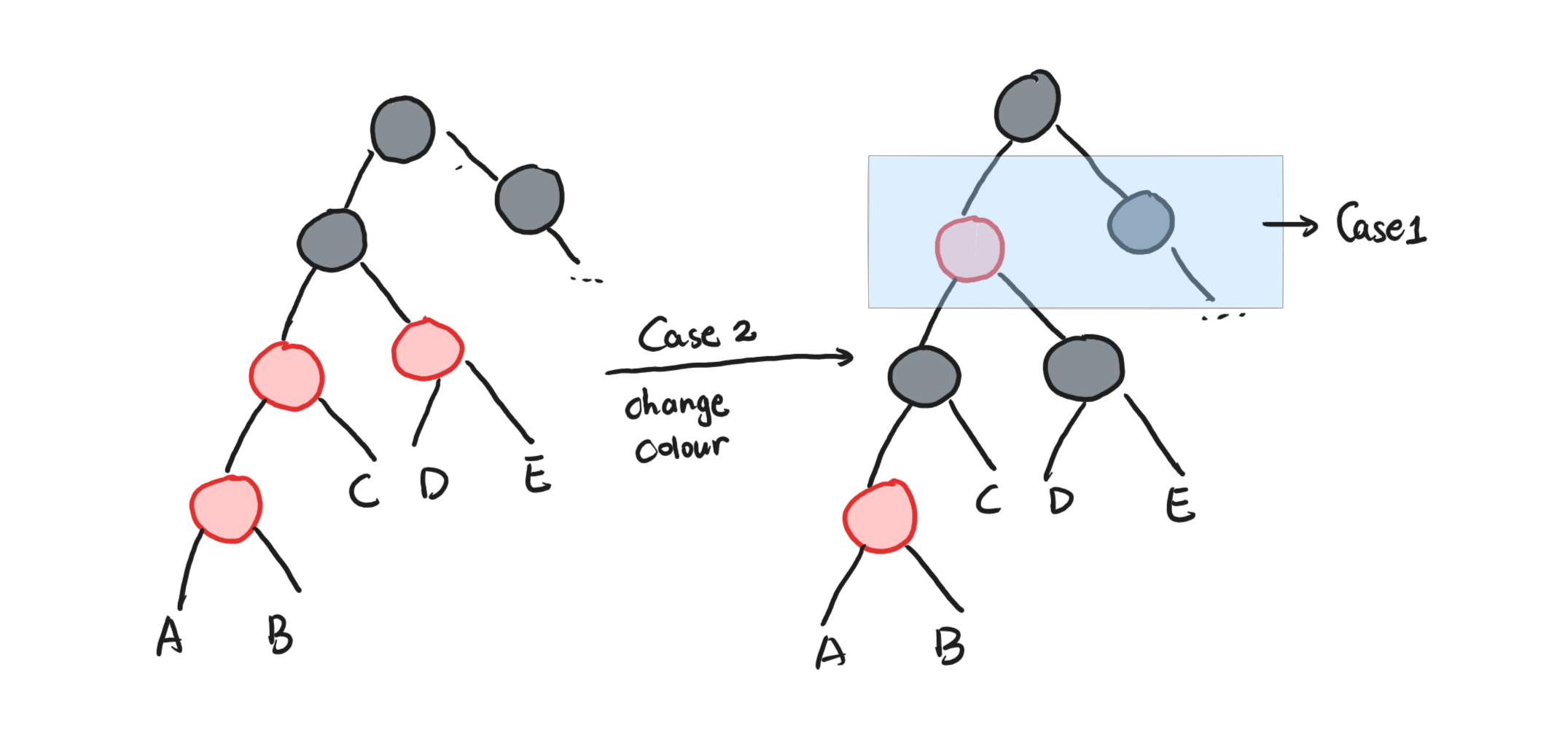
因此，我们可以归纳出插入过程的基本思路：

• 如果在空树上插入，直接将节点变黑。（因为RBT要求根节点必须是黑色的节点，这也是递归的终止条件）
• 如果是case2（叔叔节点是红色的），则祖父节点和{叔叔节点、父亲节点}之前交换颜色，同时把祖父节点作为“当前插入的节点”并不断向上递归。
• 如果是case1（叔叔节点是黑色的），则进行类似于AVL树的LLb，RRb，LRb和RLb操作，只通过一次调整就可以实现结构的平衡。

红黑树相比于传统AVL树有什么优势？

• 如果父节点是黑色节点，则不需要执行任何的操作！这带来的很大的方便。
• 如果父节点是红色的并且是Case1，则最多只需要进行一次旋转。（无需向上回溯）

我们发现，如果采用传统的递归到达叶节点插入对应元素然后再回溯改变染色，效率肯定没有AVL树高，但是我们可以在递归向下探索的时候就完成这些操作：

• 在寻找插入位置的时候，如果遇到结点$X$的两个儿子节点都是红色节点的时候，就翻转颜色。（即原来是黑色节点的$X$翻转成红色节点，同时$X$的两个儿子全部染色成红色）

  • 这样并没有修改任何一条路径上黑色节点的个数（就该次操作而言）
  • 但是可能会造成染色冲突：
    • $X$的父节点和$X$本身都是红色的节点，此时需要使用旋转操作，此时保证$X$的兄弟节点一定是黑色的（满足定义3并且$X$的父亲是红色节点）
    • 此时需要对$X$的祖父节点进行对应的旋转操作

  这里看图解：

  

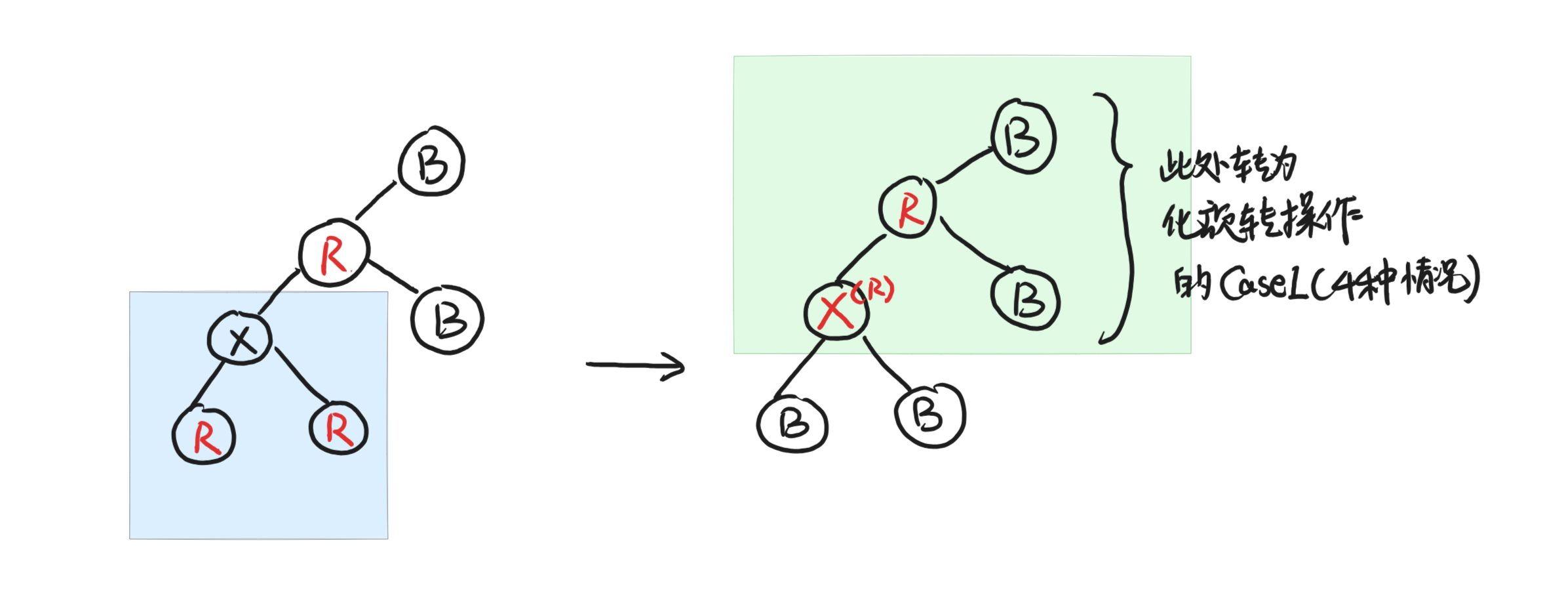
• 如果不全为红色：往下走一层

  • 如果新的$X$是红色的，那么兄弟节点是黑色的
  • 如果新的$X$是黑色的，那么兄弟节点是红色的

这样就在向下寻找叶节点的过程中，可以自动的调整红黑树的结构，转化为可以进行性能优化的尾递归，不需要再回溯了！

Delete

接下来我们来看红黑树的删除操作。

在普通的二叉查找树中，树的删除可以分为三种情况：

• 只有一个儿子
• 没有儿子
• 有两个儿子

其中前两种情况是比较简单的，因为只涉及较少的移动就可以保证有序性，对于第三种情况，我们巧妙地找到了一个替身节点，并且删除了在叶节点的替身节点。因此，在本质上，有序树的删除操作可以归纳为删除叶节点（case1,3）或者删除只有一个儿子的节点(case 2)。

如果被删除的节点是红色的，此时删除操作结束，因为没有任何违反定义的事情发生。

如果被删除的节点是黑色的，此时肯定会违反定义（每条路径上的黑色节点一样多）。

因此，我们进行自顶向下的寻找，记$X$为当前节点，$T$为兄弟节点，$P$为他们的父节点。对于每一个X，我们都尝试将它变成红色。（我们希望最后到达叶节点的时候可以直接删掉红色节点）

• $X$有两个黑色儿子
  • 需要染色+旋转
  • $T$有两个黑色儿子
    • T的颜色反转不会产生任何影响（对T的分支而言），因此之间父子之间反转颜色
  • $T$有一个外侧的红色儿子
    • 在颜色反转后会存在红色冲突，需要进行一次单旋转并且重新着色
  • $T$有一个内侧的红色儿子
    • 双旋转+重新着色
• $X$至少有一个红色儿子
  • 如果$X$不是被删除节点，直接进入下一层
    • 如果进入到红色节点处（保证存在红色节点）：万事大吉
    • 如果进入到黑色节点处：此时需要进行一次单旋转，此时$X$完成了下沉的操作并且父节点一定是黑色的（旋转）
      • 但是此时$X$仍然为黑色节点，所以需要继续操作！
  • 如果$X$是删除节点并且有两个儿子
    • 在右子树寻找替身：
      • 如果右孩子为红色，直接下移一层
      • Otherwise，左孩子为红色，此时执行LL旋转使$X$变为红色。
  • 如果$X$是删除节点并且只有一个儿子
    • 该孩子一定为红色节点（需要满足定义4）
    • 做一次单旋转交换即可。

此处还是非常复杂的。。。笔者也在努力消化。。。

Codes Implementation

AA Tree

定义

AA树是一种特殊的红黑树，添加了一个限制条件：

• 左儿子不可以是红色，