DataStructure-LinearList

Data Structure: Linear List

Abstract

This article introduces the basic data structure of linear tables, including their sequential and linked implementations. At the same time, this paper gives the definitions of the abstract base class of linear tables and the header files and member functions of the derived classes of two linear tables, and finally introduces the linear tables in STL.

接下来，我们来看数据结构中第一种数据结构，也是最简单的一种数据结构——线性结构

前置知识回顾

数据结构：建模——求解（基于数据结构的算法）

数据元素的存储：内置类型和结构体类型
数据关系的存储：
- 顺序
- 链接
- 散列
- 索引

线性结构

特点：一对一，有序

Definition：具有相同特征的节点构成的有序序列

首节点，尾节点，前继节点，后继结点

分类：

线性表（相对位置）
时间有序表（时间先后）
- 栈（3）
- 队列（4）
频率有序表（频率先后）
排序表（关键字值 Key）
- 排序

线性表

仅有节点的相互位置来确定节点的关系。0,1,2,3,4,5…，n-1,n

基本操作

创建线性表
清除线性表
求长度
插入节点，删除节点，搜索节点：O（N）
扩充数组
- 申请一个更大规模的动态数组
- 将原数组的内容拷贝到新的动态数组上
- delete掉原来的数组
- 将新数组作为新的存储区
索引
按序遍历访问

线性表的实现

顺序实现（数组）

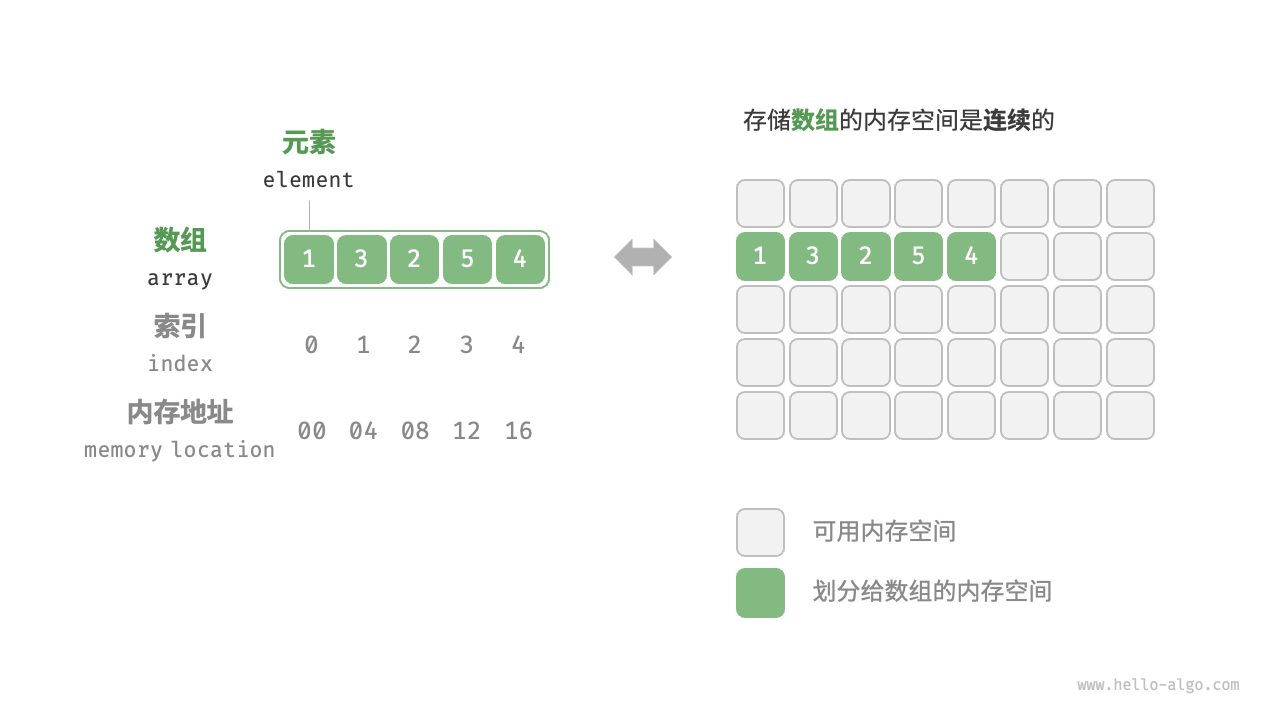
数组定义与存储方式

使用物理位置的邻接关系表示逻辑的邻接关系

优点：

无需增加额外的存储空间
方便访问表中的任意节点

缺点：插入和删除的操作效率低，空间浪费

指向线性表元素类型的指针
数组规模（最大的元素个数）
数组中的元素个数

链接实现（链表）

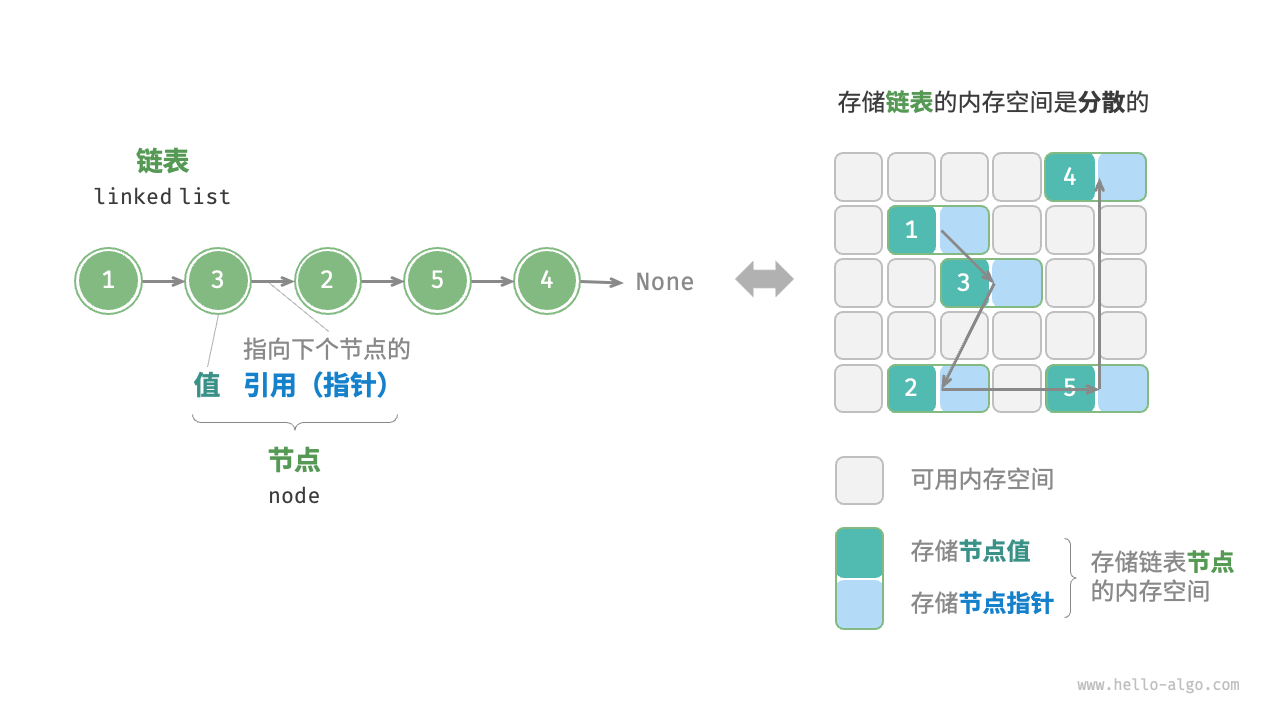
链表定义与存储方式

单链表，双链表，循环链表
头结点：保证不用对首元素进行特殊讨论

线性表的类的实现

线性表的抽象类
顺序表类
链接表类

小tips：为了方便管理，以下的类实现都会使用动态内存分配到堆上，但实际上，堆的内存更容易碎片化，效率没有栈高

线性表的抽象类

类模板

template <typename ElementType>
class List
{
public:
	virtual ~List() {}
	virtual void clear() = 0;
	virtual int length() const = 0;
	virtual void insert(int index, const ElementType& element) = 0;
	virtual void remove(int index) = 0;
	virtual int find(const ElementType& element) const = 0;
	virtual ElementType fetch(int index) const = 0;
	virtual void traverse() const = 0;
};

有关线性表抽象基类的若干说明：

=0代表在抽象基类中函数在基类中不实现，只在派生类中实现。（这也符合抽象基类的设计原理）
- =0代表这是所有派生类的共同特征，但是在不同的派生类中又有各自不同的实现方式
const代表不可以修改数据成员
在抽象基类中并未定义数据成员，因为不同的线性表的实现方式中，节点的定义是不同的：
- 在顺序表类中，节点就是直接的数据存储
- 在链接表类中，节点还需要包括指针（前驱指针和后继指针）

顺序表类

#include <iostream>
#include "Exception.h"
#include "List.h"

template <typename ElementType>
class SequentialList : public List<ElementType>
{
private:
	ElementType* elementData;
	int currentLength, totalCapacity;
	void expand();

public:
	SequentialList(int size = 10);
	~SequentialList();
	void clear();
	int length() const;
	int capacity() const;
	void insert(int index, const ElementType& element);
	void remove(int index);
	int find(const ElementType& element) const;
	ElementType fetch(int index) const;
	void traverse() const;
	ElementType back();
	void append(const ElementType& element);
	void cancel();
	void resize(int size);
	ElementType& operator[](int index);
	ElementType& operator[](int index) const;
};

template <typename ElementType>
//expand the list for a larger memory
void SequentialList<ElementType>::expand()
{
	ElementType* tempData = elementData;
	totalCapacity *= 2;
	elementData = new ElementType[totalCapacity];
	for (int i = 0; i < currentLength; i++)
		elementData[i] = tempData[i];
	delete[] tempData;
}

template <typename ElementType>
//constructor function
SequentialList<ElementType>::SequentialList(int size)
{
	currentLength = 0;
	totalCapacity = size;
	elementData = new ElementType[size];
}

template <typename ElementType>
//destructor function
SequentialList<ElementType>::~SequentialList()
{
	delete[] elementData;
}

template <typename ElementType>
//clear the list
void SequentialList<ElementType>::clear()
{
	currentLength = 0;
}

template <typename ElementType>
//the const means the function cannot modify the value of the statics of the object
int SequentialList<ElementType>::length() const
{
	return currentLength;
}

template <typename ElementType>
int SequentialList<ElementType>::capacity() const
{
	return totalCapacity;
}

template <typename ElementType>
//insert the value on a certain index
void SequentialList<ElementType>::insert(int index, const ElementType& element)
{
	if (index < 0 || index > currentLength)//the index is INVALID
		throw IndexExceed();
	if (currentLength == totalCapacity)
		expand();
	for (int i = currentLength; i > index; i--)
		elementData[i] = elementData[i - 1];
    //move each element backwards
	elementData[index] = element;
	currentLength++;
}

template <typename ElementType>
//delete the element on a certain index
void SequentialList<ElementType>::remove(int index)
{
	if (index < 0 || index >= currentLength)
		throw IndexExceed();
	for (int i = index; i < currentLength - 1; i++)
		elementData[i] = elementData[i + 1];
	currentLength--;
}

template <typename ElementType>
int SequentialList<ElementType>::find(const ElementType& element) const
{
	int i;
	for (i = 0; i < currentLength && elementData[i] != element; i++)
		;
    //the loop end if the tarverse ends or the target element has been found
	if (i == currentLength)
		return -1;
	else
		return i;
}

template <typename ElementType>
ElementType SequentialList<ElementType>::fetch(int index) const
{
	if (index < 0 || index >= currentLength)
		throw IndexExceed();
	return elementData[index];
}

template <typename ElementType>
void SequentialList<ElementType>::traverse() const
{
	for (int i = 0; i < currentLength; i++)
		std::cout << elementData[i] << "\t";
	std::cout << "\n";
}

template <typename ElementType>
ElementType SequentialList<ElementType>::back()
    //return the last element
{
	return elementData[currentLength - 1];
}

template <typename ElementType>
void SequentialList<ElementType>::append(const ElementType& element)
{
	insert(currentLength, element);
}

template <typename ElementType>
void SequentialList<ElementType>::cancel()
{
	remove(currentLength - 1);
}

template <typename ElementType>
void SequentialList<ElementType>::resize(int size)
{
	if (size <= totalCapacity)
		throw InvalidModify();
	ElementType* tempData = elementData;
	totalCapacity = size;
	elementData = new ElementType[totalCapacity];
	for (int i = 0; i < currentLength; i++)
		elementData[i] = tempData[i];
	delete[] tempData;
}

template <typename ElementType>
ElementType& SequentialList<ElementType>::operator[](int index)
{
	if (index < 0 || index >= currentLength)
		throw IndexExceed();
	return elementData[index];
}

template <typename ElementType>
ElementType& SequentialList<ElementType>::operator[](int index) const
    //Operator Overloading with const
{
	if (index < 0 || index >= currentLength)
		throw IndexExceed();
	return elementData[index];
}

单链表类

#include <iostream>
#include "Exception.h"
#include "List.h"

template <typename ElementType>
class SingleLinkedList : public List<ElementType>
{
private:
	struct ListNode
	{
		ElementType data;
		ListNode* next;
		ListNode() : data(), next(nullptr) {}
		ListNode(const ElementType& _data, ListNode* _next = nullptr) : data(_data), next(_next) {}
        //constructor
		~ListNode() {}
        //destructor
	};
	ListNode* head;
	int currentLength;
	ListNode* place(int index) const;

public:
	SingleLinkedList();
	~SingleLinkedList();
	void clear();
	int length() const;
	void insert(int index, const ElementType& element);
	void remove(int index);
	int find(const ElementType& element) const;
	ElementType fetch(int index) const;
	void traverse() const;
	void append(const ElementType& element);
	void erase(int index);
};

template <typename ElementType>
typename SingleLinkedList<ElementType>::ListNode* SingleLinkedList<ElementType>::place(int index) const
{
	ListNode* p = head;
	while (index >= 0)
	{
		index--;
		p = p->next;
	}
	return p;
}

template <typename ElementType>
SingleLinkedList<ElementType>::SingleLinkedList()
{
	head = new ListNode;
	currentLength = 0;
}

template <typename ElementType>
SingleLinkedList<ElementType>::~SingleLinkedList()
{
	clear();
	delete head;
}

template <typename ElementType>
void SingleLinkedList<ElementType>::clear()
{
	ListNode* p = head->next, * q;
	head->next = nullptr;
	while (p != nullptr)
	{
		q = p->next;
		delete p;
		p = q;
	}
	currentLength = 0;
}

template <typename ElementType>
int SingleLinkedList<ElementType>::length() const
{
	return currentLength;
}

template <typename ElementType>
void SingleLinkedList<ElementType>::insert(int index, const ElementType& element)
{
	if (index < 0 || index > currentLength)
		throw IndexExceed();
	ListNode* p = place(index - 1);
	p->next = new ListNode(element, p->next);
	currentLength++;
}

template <typename ElementType>
void SingleLinkedList<ElementType>::remove(int index)
{
	if (index < 0 || index >= currentLength)
		throw IndexExceed();
	ListNode* p = place(index - 1), * q = p->next;
	p->next = q->next;
	delete q;
	currentLength--;
}

template <typename ElementType>
int SingleLinkedList<ElementType>::find(const ElementType& element) const
{
	ListNode* p = head->next;
	int index = 0;
	while (p != nullptr && p->data != element)
	{
		p = p->next;
		index++;
	}
	if (p == nullptr)
		return -1;
	else
		return index;
}

template <typename ElementType>
ElementType SingleLinkedList<ElementType>::fetch(int index) const
{
	if (index < 0 || index >= currentLength)
		throw IndexExceed();
	return place(index)->data;
}

template <typename ElementType>
void SingleLinkedList<ElementType>::traverse() const
{
	ListNode* p = head->next;
	while (p != nullptr)
	{
		std::cout << p->data << "\t";
		p = p->next;
	}
	std::cout << "\n";
}

template <typename ElementType>
void SingleLinkedList<ElementType>::append(const ElementType& element)
{
	insert(currentLength, element);
}

template <typename ElementType>
void SingleLinkedList<ElementType>::erase(int index)
{
	if (index < 0 || index >= currentLength)
		throw IndexExceed();
	ListNode* p = place(index - 1), * q = p->next;
	ElementType target = q->data;
	p->next = q->next;
	delete q;
	int count = 1;
	for (p = head; p->next != nullptr;)
	{
		if (p->next->data == target)
		{
			q = p->next;
			p->next = q->next;
			delete q;
			count++;
		}
		else
			p = p->next;
	}
	currentLength -= count;
}

STL：Standard Template Library

泛型思想：

把算法和数据类型分离：模版函数
把算法和容器分离：STL和迭代器
把容器和数据类型分离：模板类

容器，迭代器，算法

迭代器：为每一种容器定义的表示其元素相对位置的类型，迭代器对象相当于指向容器中指向对象的指针，他将容器中对象的位置信息封装了起来。从使用者的角度而言，可以把迭代器当作一种抽象的指针。

每个容器提供两种迭代器，const和非const

补充知识点：迭代器中重载的常见运算符

在 C++ 中，迭代器通常会重载一组运算符，以便像指针一样使用它们。这些运算符使得迭代器能够在容器中进行遍历、索引以及修改数据。具体来说，常见的迭代器会重载以下运算符：

解引用运算符 \*

作用：访问迭代器当前指向的元素。

示例

1
2
3

std::vector<int> v = {1, 2, 3, 4};
auto it = v.begin();
std::cout << *it;  // 输出 1，指向第一个元素

箭头运算符 ->

作用：通过迭代器访问指向对象的成员（适用于指向对象的迭代器，如 std::map、std::unordered_map 等）。

示例

1
2
3

std::vector<std::pair<int, int>> v = {{1, 2}, {3, 4}};
auto it = v.begin();
std::cout << it->first << ", " << it->second;  // 输出 1, 2

前置递增运算符 ++

作用：将迭代器向前移动一个位置，指向容器中的下一个元素。

示例

std::vector<int> v = {1, 2, 3, 4};
auto it = v.begin();
++it;  // 将迭代器移动到第二个元素
std::cout << *it;  // 输出 2

后置递增运算符 ++

作用：与前置递增运算符类似，但它会返回移动前的迭代器，通常用于赋值操作中。

示例

std::vector<int> v = {1, 2, 3, 4};
auto it = v.begin();
auto it_copy = it++;  // it_copy 是移动前的迭代器，it 会向前移动
std::cout << *it_copy;  // 输出 1
std::cout << *it;       // 输出 2

前置递减运算符 --

作用：将迭代器向后移动一个位置，指向容器中的前一个元素。

示例

std::vector<int> v = {1, 2, 3, 4};
auto it = v.end();
--it;  // 将迭代器移动到最后一个元素
std::cout << *it;  // 输出 4

后置递减运算符 --

作用：与前置递减运算符类似，但它会返回移动前的迭代器。

示例

std::vector<int> v = {1, 2, 3, 4};
auto it = v.end();
auto it_copy = it--;  // it_copy 是移动前的迭代器，it 会向后移动
std::cout << *it_copy;  // 输出 4
std::cout << *it;       // 输出 3

比较运算符 == 和 !=

作用：比较两个迭代器是否相等。对于容器中的元素，迭代器 == 表示它们指向同一个位置，!= 表示它们指向不同的位置。

示例

std::vector<int> v = {1, 2, 3, 4};
auto it1 = v.begin();
auto it2 = v.begin();
auto it3 = v.end();

std::cout << (it1 == it2);  // 输出 1 (true)
std::cout << (it1 != it3);  // 输出 1 (true)

加法运算符 +（某些迭代器）

作用：允许迭代器跳过多个元素，通常返回一个新的迭代器。

示例

std::vector<int> v = {1, 2, 3, 4};
auto it = v.begin();
it = it + 2;  // 跳过两个元素，指向第三个元素
std::cout << *it;  // 输出 3

减法运算符 -（某些迭代器）

作用：允许迭代器向回跳过多个元素。

示例

（对于随机访问迭代器，如 std::vector）

std::vector<int> v = {1, 2, 3, 4};
auto it = v.end();
it = it - 2;  // 向回跳过两个元素，指向第三个元素
std::cout << *it;  // 输出 3

加法赋值运算符 += 和减法赋值运算符 -=

作用：使迭代器向前或向后移动指定的步数。

示例

std::vector<int> v = {1, 2, 3, 4};
auto it = v.begin();
it += 2;  // 向前移动两个位置，指向第三个元素
std::cout << *it;  // 输出 3
it -= 1;  // 向后移动一个位置
std::cout << *it;  // 输出 2

下标运算符 []（适用于随机访问迭代器）

作用：通过下标访问迭代器当前所指向的元素。

示例

（对于随机访问迭代器，如 std::vector）：

1
2
3

std::vector<int> v = {1, 2, 3, 4};
auto it = v.begin();
std::cout << it[2];  // 输出 3

注意：8,9,10,11一般适用于随机访问迭代器（支持任意位置的跳跃访问和直接跳转，因此可以实现高效的前后移动），对应的容器有线性容器，如 std::vector、std::deque、std::array 和 std::string，而std::set 和 **std::map**（以及它们的 unordered 版本），这些容器的迭代器也不支持随机访问，因为它们通常是基于树或哈希表的结构。

STL中的线性表

在 C++ 标准库中，std::vector 和 std::list 是两个常用的容器类，它们分别代表动态数组和双向链表。虽然它们都实现了 std::container 的接口，但它们的内部结构和适用场景不同，因此提供的库函数也有所不同。

1. `std::vector` 类的常见库函数

std::vector 是一个动态数组容器，支持随机访问。它非常适合用来存储需要频繁随机访问的数据。常见的成员函数包括：

1.1 构造函数和赋值操作

**vector()**：默认构造函数，创建一个空的 vector。
**vector(n)**：构造一个包含 n 个默认值的 vector。
**vector(n, value)**：构造一个包含 n 个值为 value 的 vector。
**vector(begin, end)**：使用范围 [begin, end) 的元素来构造 vector。
**operator=**：赋值操作符，用于将一个 vector 赋值给另一个。

1.2 元素访问

**operator[]**：通过下标访问元素。
**at()**：通过下标访问元素，但会进行边界检查。
**front()**：返回第一个元素。
**back()**：返回最后一个元素。
**data()**：返回指向第一个元素的指针。

1.3 容量操作

**size()**：返回 vector 中元素的个数。
**capacity()**：返回 vector 的容量（即 vector 可以存储的最大元素个数，不一定等于 size()）。
**empty()**：检查 vector 是否为空。
**reserve()**：预留至少可以容纳 n 个元素的空间。
**shrink_to_fit()**：请求减少 vector 的容量，使其尽可能接近 size()，但不保证立即生效。

1.4 修改操作

**push_back()**：在 vector 的末尾添加元素。
**pop_back()**：删除 vector 中的最后一个元素。
**insert()**：在指定位置插入元素。
**erase()**：删除指定位置的元素。
**clear()**：删除 vector 中的所有元素。

1.5 迭代器和算法

**begin()**：返回指向 vector 第一个元素的迭代器。
**end()**：返回指向 vector 末尾元素之后位置的迭代器。
**rbegin()**：返回指向 vector 最后一个元素的反向迭代器。

#include <iostream>
#include <vector>

int main() {
    std::vector<int> v = {10, 20, 30, 40, 50};

    // 使用反向迭代器进行遍历
    for (auto it = v.rbegin(); it != v.rend(); ++it) {
        std::cout << *it << " ";  // 输出: 50 40 30 20 10
    }

    return 0;
}

**rend()**：返回指向 vector 第一个元素之前的反向迭代器。

1.6 其他操作

**swap()**：交换两个 vector 的内容。
**resize()**：改变 vector 的大小，如果新大小大于当前大小，新增的元素会用默认值初始化。
**emplace_back()**：在 vector 末尾构造一个元素。
**emplace()**：在指定位置构造一个元素。

2. `std::list` 类的常见库函数

std::list 是一个双向链表容器，适合用来执行大量的插入和删除操作。由于是链表结构，std::list 不支持随机访问，只能进行顺序访问。常见的成员函数包括：

2.1 构造函数和赋值操作

**list()**：默认构造函数，创建一个空的 list。
**list(n)**：构造一个包含 n 个默认值的 list。
**list(n, value)**：构造一个包含 n 个值为 value 的 list。
**list(begin, end)**：使用范围 [begin, end) 的元素来构造 list。
**operator=**：赋值操作符，用于将一个 list 赋值给另一个。

2.2 元素访问

**front()**：返回 list 中的第一个元素。
**back()**：返回 list 中的最后一个元素。

2.3 容量操作

**size()**：返回 list 中元素的个数。
**empty()**：检查 list 是否为空。

2.4 修改操作

**push_front()**：将元素添加到 list 的前面。
**push_back()**：将元素添加到 list 的末尾。
**pop_front()**：删除 list 中的第一个元素。
**pop_back()**：删除 list 中的最后一个元素。
**insert()**：在指定位置插入一个元素。
**erase()**：删除指定位置的元素。
**remove()**：删除所有等于指定值的元素。
**clear()**：删除 list 中的所有元素。

2.5 迭代器和算法

**begin()**：返回指向 list 第一个元素的迭代器。
**end()**：返回指向 list 末尾元素之后位置的迭代器。
**rbegin()**：返回指向 list 最后一个元素的反向迭代器。
**rend()**：返回指向 list 第一个元素之前的反向迭代器。

2.6 其他操作

**swap()**：交换两个 list 的内容。
**resize()**：改变 list 的大小。如果新大小大于当前大小，新增的元素会使用默认值初始化。
**unique()**：删除 list 中相邻的重复元素。

3. 总结

操作	`std::vector`	`std::list`
构造函数	`vector()`, `vector(n)`, `vector(n, value)`	`list()`, `list(n)`, `list(n, value)`
访问元素	`operator[]`, `at()`, `front()`, `back()`	`front()`, `back()`
容量操作	`size()`, `capacity()`, `reserve()`, `shrink_to_fit()`	`size()`, `empty()`
修改操作	`push_back()`, `pop_back()`, `insert()`, `erase()`, `clear()`	`push_front()`, `push_back()`, `pop_front()`, `pop_back()`, `insert()`, `erase()`, `clear()`
迭代器操作	`begin()`, `end()`, `rbegin()`, `rend()`	`begin()`, `end()`, `rbegin()`, `rend()`
其他操作	`resize()`, `swap()`, `emplace_back()`, `emplace()`	`swap()`, `resize()`, `unique()`, `remove()`

std::vector 适合频繁的随机访问操作和需要动态扩展大小的场景，但在插入或删除操作上可能效率较低。
std::list 适合需要频繁插入和删除操作的场景，尤其是在容器中间的位置，虽然其访问速度较慢。

选择使用哪个容器，取决于应用场景的需求：如果需要高效的随机访问，使用 std::vector；如果需要频繁地在容器中间插入和删除元素，使用 std::list。

补充知识：内存和缓存：从硬件视角看数据结构的选择

以下内容整理自《Hello 算法》

首先抛出观点：物理结构在很大程度上决定了程序对内存和缓存的使用效率。

计算机存储设备

计算机中包括三种类型的存储设备：硬盘（hard disk）、内存（random-access memory, RAM）、缓存（cache memory）。表 4-2 展示了它们在计算机系统中的不同角色和性能特点。

表 4-2 计算机的存储设备

	硬盘	内存	缓存
用途	长期存储数据，包括操作系统、程序、文件等	临时存储当前运行的程序和正在处理的数据	存储经常访问的数据和指令，减少 CPU 访问内存的次数
易失性	断电后数据不会丢失	断电后数据会丢失	断电后数据会丢失
容量	较大，TB 级别	较小，GB 级别	非常小，MB 级别
速度	较慢，几百到几千 MB/s	较快，几十 GB/s	非常快，几十到几百 GB/s
价格	较便宜，几毛到几元 / GB	较贵，几十到几百元 / GB	非常贵，随 CPU 打包计价

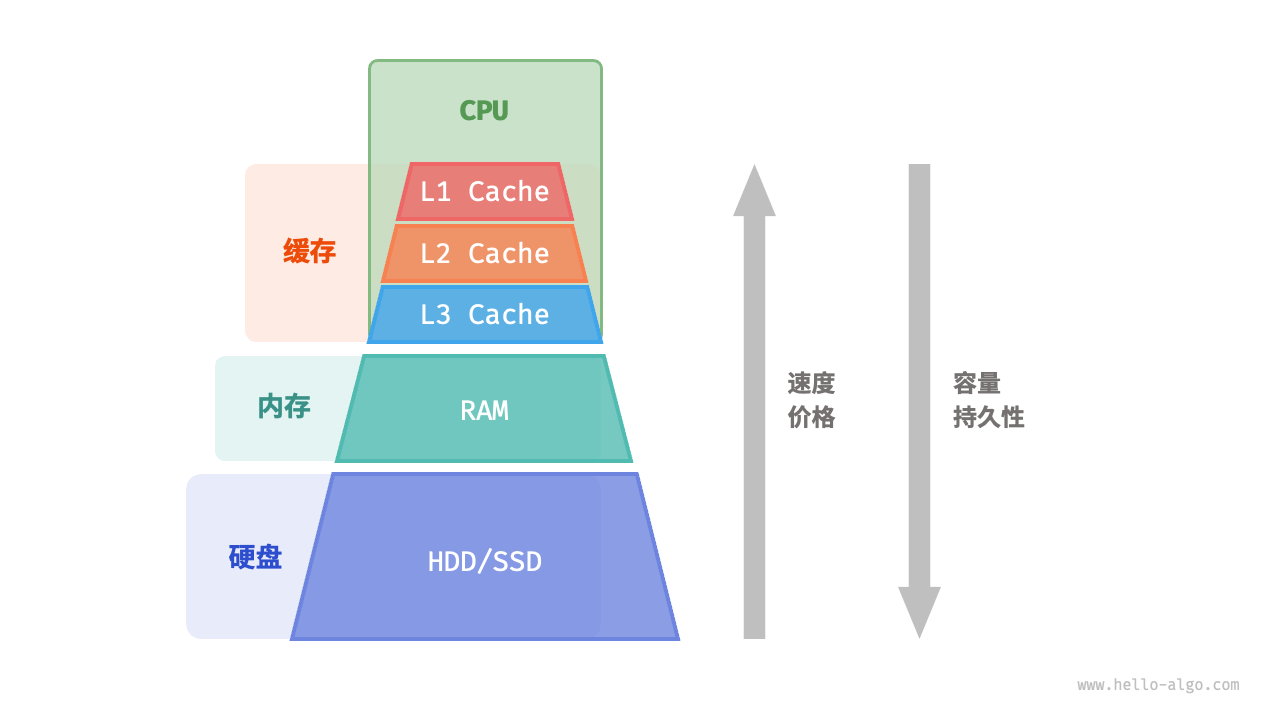
计算机存储系统 Hello算法

计算机的存储层次结构体现了在速度，容量和成本三者之间的精妙平衡。

数据结构的内存效率

在上文我们已经比较过数组和链表在内存角度的优缺点：

数组元素在内存上排列紧密，但是需要一整块内存进行存储。查找效率高但插入，删除效率低。
链表元素在内存上分散排布，但需要额外储存指针的值。插入、删除效率高但遍历效率低。
- 链表还有一个比较大的弊端：如果在链表中频繁的插入和删除，会导致内存的碎片化，是内存的使用效率降低。

数据结构的缓存效率（Additional）

缓存虽然在空间容量上远小于内存，但它比内存快得多，在程序执行速度上起着至关重要的作用。由于缓存的容量有限，只能存储一小部分频繁访问的数据，因此当 CPU 尝试访问的数据不在缓存中时，就会发生缓存未命中（cache miss），此时 CPU 不得不从速度较慢的内存中加载所需数据。

显然，“缓存未命中”越少，CPU 读写数据的效率就越高，程序性能也就越好。我们将 CPU 从缓存中成功获取数据的比例称为缓存命中率（cache hit rate），这个指标通常用来衡量缓存效率。

实际上，数组和链表对缓存的利用效率是不同的，主要体现在以下几个方面。

占用空间：链表元素比数组元素占用空间更多，导致缓存中容纳的有效数据量更少。
缓存行：链表数据分散在内存各处，而缓存是“按行加载”的，因此加载到无效数据的比例更高。
预取机制：数组比链表的数据访问模式更具“可预测性”，即系统更容易猜出即将被加载的数据。
空间局部性：数组被存储在集中的内存空间中，因此被加载数据附近的数据更有可能即将被访问。

总体而言，数组具有更高的缓存命中率，因此它在操作效率上通常优于链表。这使得在解决算法问题时，基于数组实现的数据结构往往更受欢迎。

线性表的应用

大整数处理

多项式求和

约瑟夫环问题

动态内存管理

Algorithm

#tutorial #C/C++ #Finished #Data Structure #Linear List

DataStructure-LinearList

https://xiyuanyang-code.github.io/posts/DataStructure-LinearList/

Author

Xiyuan Yang

Posted on

December 18, 2024

Updated on

March 30, 2025

Licensed under

DataStructure-Stack Previous

DataStructure-Tutorial Next

DataStructure-LinearList

Data Structure: Linear List

Abstract

线性结构

线性表

基本操作

线性表的实现

顺序实现（数组）

链接实现（链表 ）

线性表的类的实现

线性表的抽象类

顺序表类

单链表类

STL：Standard Template Library

STL中的线性表

1. std::vector 类的常见库函数

1.1 构造函数和赋值操作

1.2 元素访问

1.3 容量操作

1.4 修改操作

1.5 迭代器和算法

1.6 其他操作

2. std::list 类的常见库函数

2.1 构造函数和赋值操作

2.2 元素访问

2.3 容量操作

2.4 修改操作

2.5 迭代器和算法

2.6 其他操作

3. 总结

线性表的应用

大整数处理

多项式求和

约瑟夫环问题

动态内存管理

链接实现（链表）

1. `std::vector` 类的常见库函数

2. `std::list` 类的常见库函数