DataStructure Graph SCC

Several Algorithms for Strong Connected Components

Introduction

问题很简单，给定图$G = (V, E)$，请设计高效的算法找出联通分量。

• 对于无向图，扫一次DFS，生成的DFS树的集合就是联通分量。
• 对于有向图，即强联通分量 (Strong Connected Components, SCC)的寻找非常的困难，需要高级且独特的算法设计。

下面介绍经典的两种寻找SCC的算法：Tarjan算法和Kosaraju算法。

Kosaraju

• 从任意结点开始对有向图$G$进行深度优先搜索，得到一个深度优先森林。
• 将节点遍历：按照生成树的次序 + 对每一棵树上的节点进行后序遍历
• 将图$G$逆向得到$G_r$。
• 从编号最大的节点开始深度优先搜索$G_r$,得到的森林就是原图的强联通分量。

Thm

• $x$ is the root for the tree which contains $v$ in $G_r$, then $\exists x \to v \in G_r \text{ and } v \to x \in G$.
• $x$ is the root for the tree which contains $w$ in $G_r$, then $\exists x \to w \in G_r \text{ and } w \to x \in G$.

Then it suffices to prove:

• If $v$ and $w$ are in the same BFS tree for $G_r$, then $\exists v \to w \text{ and } w \to v \in G$.

Hence, we only need to prove:

$x$ is the root for the tree which contains $v$ in $G_r$, then $\exists x \to v \in G_r \text{ and } v \to x \in G$.

• For $x$ is the root node, there exists a path from $x$ to $v$ in $G_r$.
• For $x$ is the root node, the index for $x$ is greater than $v$. Hence, all work of $v$ will be finished before $x$.
• Hence, there exists a path from $v$ to $x$. ($v$ finishes before $x$)

Tarjan

DFS Tree

在DFS过程中，按照生成的顺序会生成一颗结构良好的DFS树。DFS得到的序列（DFS序并不能保证相邻节点一定有边相连），但是DFS树的节点一定都是图中的节点，换句话说，DFS树在本质上就是一个在中序遍历上完全等价的树。

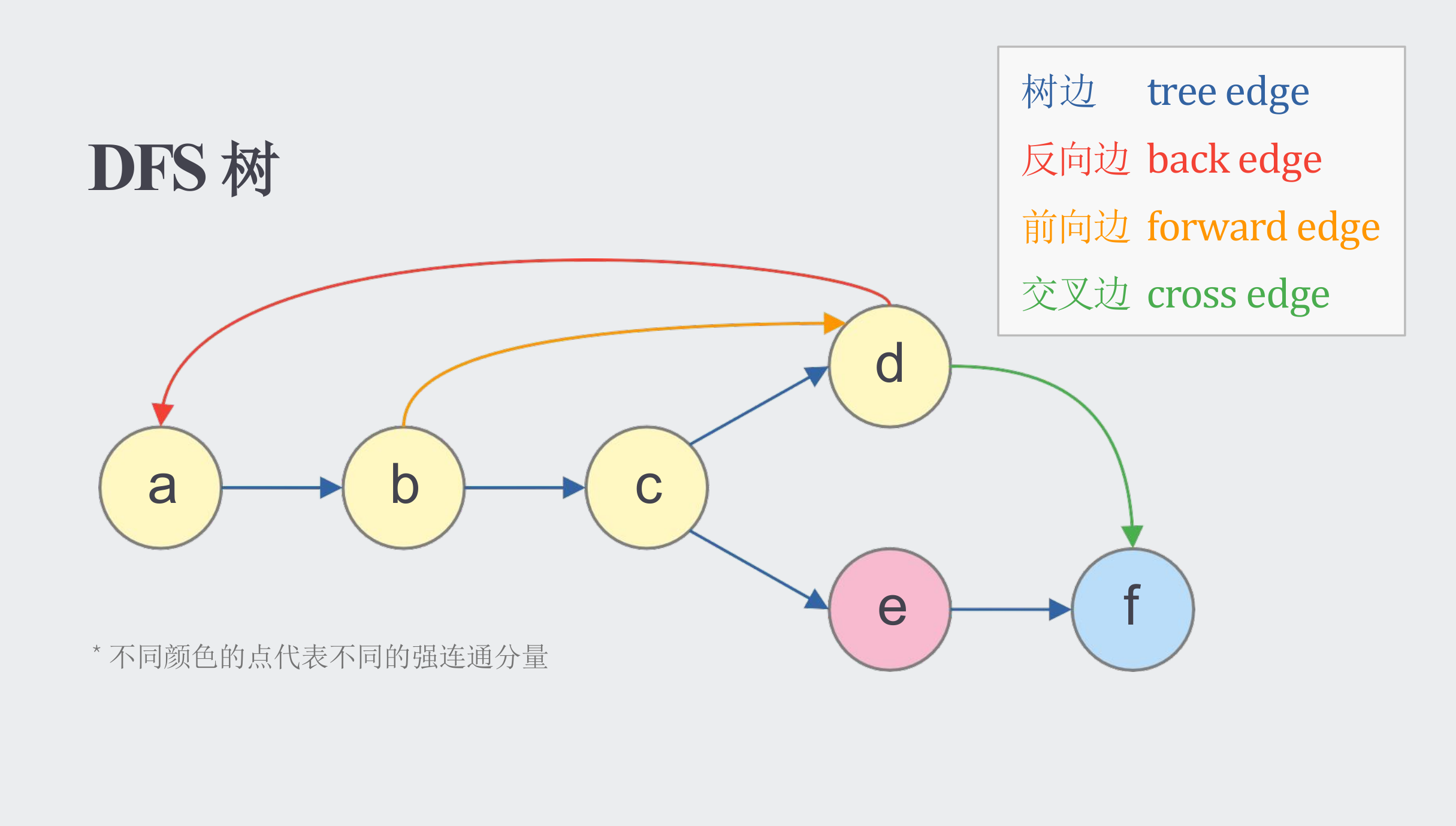
但是很显然，一颗DFS树上的顶点不代表联通。我们需要考虑不在DFS树上的边，例如这里的：

• 反向边
• 前向边
• 交叉边

Lemma

考虑$u$节点的强联通分量，我们可以证明：如果$u$是强联通分量等价类中dfs序最小的节点，那么在DFS树中$u$的其他强联通节点一定都在以$u$为根节点的子树上。

Algorithm

Tarjan算法通过一次DFS遍历，利用栈和时间戳来识别SCC。其核心思想是：

• 每个SCC在DFS树中会形成一棵子树。
• 通过维护访问顺序（dfn）和能回溯到的最早节点（low），可以判断哪些节点属于同一个SCC。
• $dfn[u]$代表了节点$u$的DFS序，$low[u]$代表了在$u$的子树中能够回溯到的最早的已经在栈中的结点。
  • 我们要求从v到low(v)的过程中最多只能有一条非树边。

我们在全程将会维护一个栈，每次把搜索树中未处理的节点加入栈中。

栈（stack）用于动态存储当前DFS路径上的节点，并帮助判断哪些节点属于同一个强连通分量（SCC）。它的核心作用是：

1. 记录当前DFS遍历的路径（可能构成SCC的候选节点）。
2. 在发现SCC的根节点时，弹出该SCC的所有节点。

当节点 u 第一次被DFS访问时（即 dfn[u] 被赋值后），立即入栈

如何判断弹栈的时机？

当发现 dfn[u] == low[u] 时，说明 u 是一个SCC的根节点，此时：

1. 从栈顶开始弹出节点，直到 u 被弹出。
2. 弹出的所有节点构成一个SCC。

因为low在本质上就是在维护栈的顺序性，或者说DFS树的顺序性。当上述条件成立，即代表节点$u$就是其强联通分量在DFS树中的跟节点。而后入栈的都是节点$u$的子树部分，和其属于相同的SCC。

• 如果需要递归访问$v$,在访问结束之后需要更新$low$的值，因为有可能节点$v$通过非树边走向了更前面的节点。
• 如果$v$已经被访问过了（说明$(u,v)$是非树边）
  • 如果$v$是$u$的祖先：
    • 此时 dfn[v] < dfn[u]，更新 low[u] = min(low[u], dfn[v])，表示 u 可以回溯到更早的节点 v。
  • 如果$(u,v)$是一条横线边：
    • dfn[v] 是严格的时间戳，表示 v 的访问顺序。
    • 如果使用 low[v]，可能会错误地跨SCC传递 low 值（因为 v 可能属于其他已处理的SCC）。
    • 核心原则：
      • 只有栈内节点（in_stack[v] == True）才能参与当前SCC的构成。
      • 用 dfn[v] 保证只利用当前DFS路径上的信息，避免污染其他SCC。

时间复杂度：$O(|V| + |E|)$

Applications

通过SCC缩点（这些点在联通性上是完全等价的），我们可以将有向图转化为DAG！

例如下面的图：

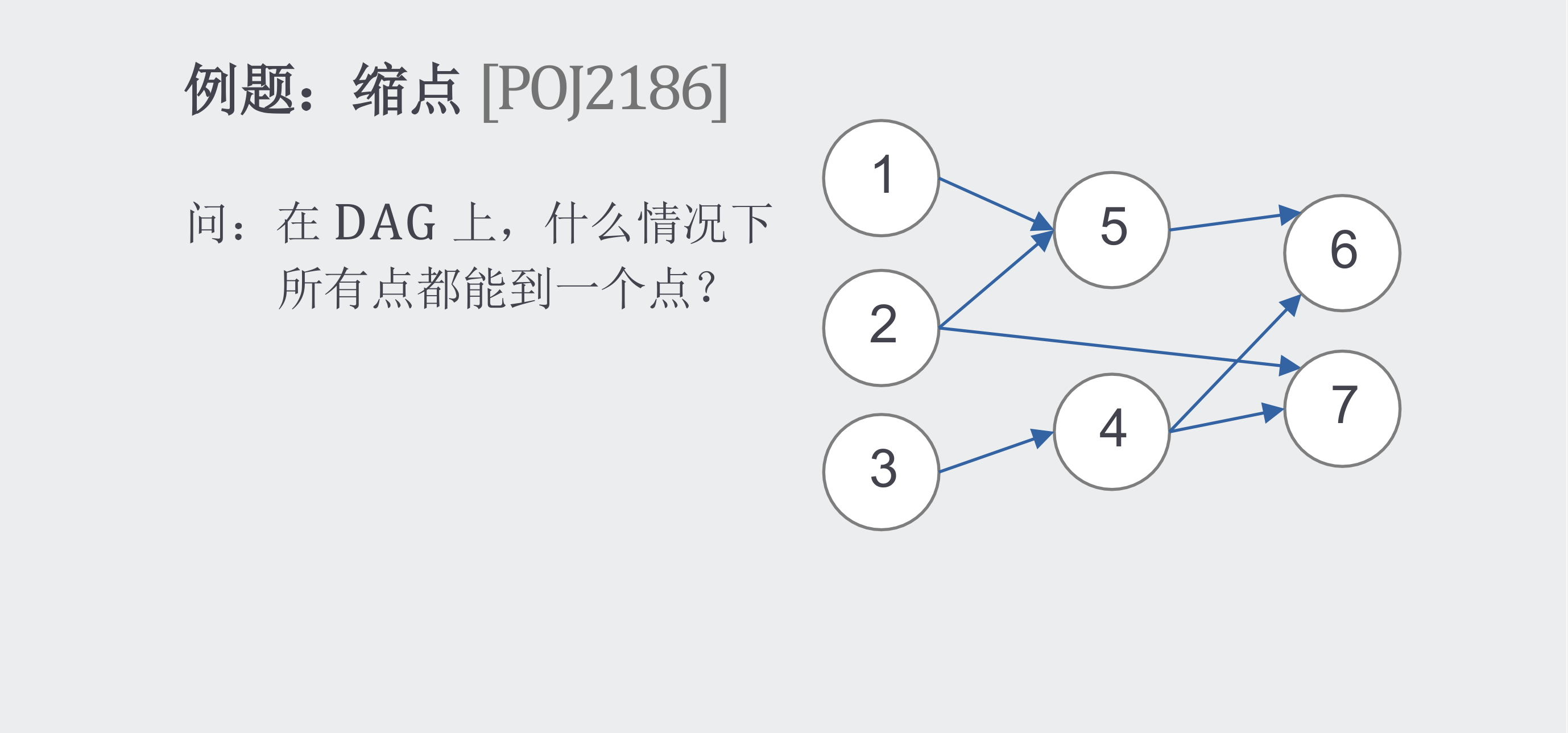
要在缩点后证明点$v$是唯一出度为0的点。

DAG 就是一个偏序关系！（自反 反对称 传递）

若从 u 能到 v 则 u ⩾ v

偏序关系中，若存在最小元，则最小元唯一，且不大于等于任何其他元素。

DAG 中，若存在一个所有点都可达的点，则这个点唯一，且不能到达除自身外任何点