DataStructure Graph Introduction

Graph Theory

Introduction

Welcome to the world of Graph!

接下来将会更新一系列有关图论的内容，聚焦于经典图论算法和图论的相关应用。本文首先需要对图给出数学化的定义，并以此为基础建立图的数据结构。

Lots of Definition…

$G = (V, E)$, where $V$ represents the set of all vertices $v$ and $E$ represents the set of all edges $e$.

$E \subseteq V \times V$ (For directed graph)

• 有向图 & 无向图
• 有向边 & 无向边
  • 一般有向边使用$<a, b>$来表示，而无向边由$(a,b)$来表示。
• 出度 & 入度（都是对于有向边而言）& 度
• 前驱节点 & 后继节点（针对有向图而言）
• 有向完全图 & 无向完全图
• 权重：加权有向图 & 加权无向图，又称为网络
• 路径和路径的长度表示（可以使用权重之和或者经过节点的个数）
• 简单路径：不允许顶点的重复
  • 这里不同地方的定义不同，也有定义成不允许重复的边的。
• 简单环路：简单路径的起点和终点相同
• 子图
• 连通图 & 连通分量
• 强连通图 & 强联通分量
• 生成树 (Spanning Tree) ：
  • 图的极小联通子图，并且要求具有树的结构。
    • 如果去掉一条边，这个子图将不连通（树形结构是其最小的可能联通结构）
    • 如果增加一条新的边$(v_i,v_j)$，因顶点$v_i$和$v_j$之间原本连通，即存在一条路径，加上新加的这条边便形成了回路，有回路就不再是树
    • 每一个连通图至少有一种生成树，但是有可能不止一颗
  • 包含$n$个顶点，$n - 1$条边，即$|V| = n,\ |E| = n - 1$
    • 树形结构要求每一个节点都需要有唯一的前驱结点（根节点除外），因此满足$|V| = |E| + 1$的性质！

图的存储和运算实现

邻接矩阵

• 使用一个一维数组来储存集合$V$，即图中的所有的点。

• 使用一个二维数组$A[i][j]$来储存集合$E$，$A[i][j]$代表$v_i$和$v_j$两个点的链接情况（或者权重）

• 好处就是使用数组可以实现$O(1)$的查询速度，但是很难插入新的点（因为顺序存储），并且空间开销很大。

在有向图中，其邻接矩阵

• 某一行中所有1的个数，就是相应行顶点的出度；
• 某一列中所有1的个数，就是相应列顶点的入度。

在无向图中（不考虑权重），写出完整的邻接矩阵实际上是一个对称矩阵，因此可以只存储上三角矩阵。

邻接表

为了尽可能节省空间，我们可以使用链接实现来优化存储。

• 使用一个一维数组来储存集合$V$中的每一个点。
  • 邻接于同一个顶点的所有边形成一条单链表（对于无向图）
  • 对于有向图，自同一个顶点出发的所有边形成一条单链表
• 即链表和数组存储的形式（怎么那么像哈希表哈哈哈哈）
  • 方便计算出度，不方便计算入度($O(|V| + |E|)$)
  • 支持插入和删除的操作
  • 查询为$O(N)$
• Time complexity: $O(|V| + |E|)$
• 当然，也有逆邻接表

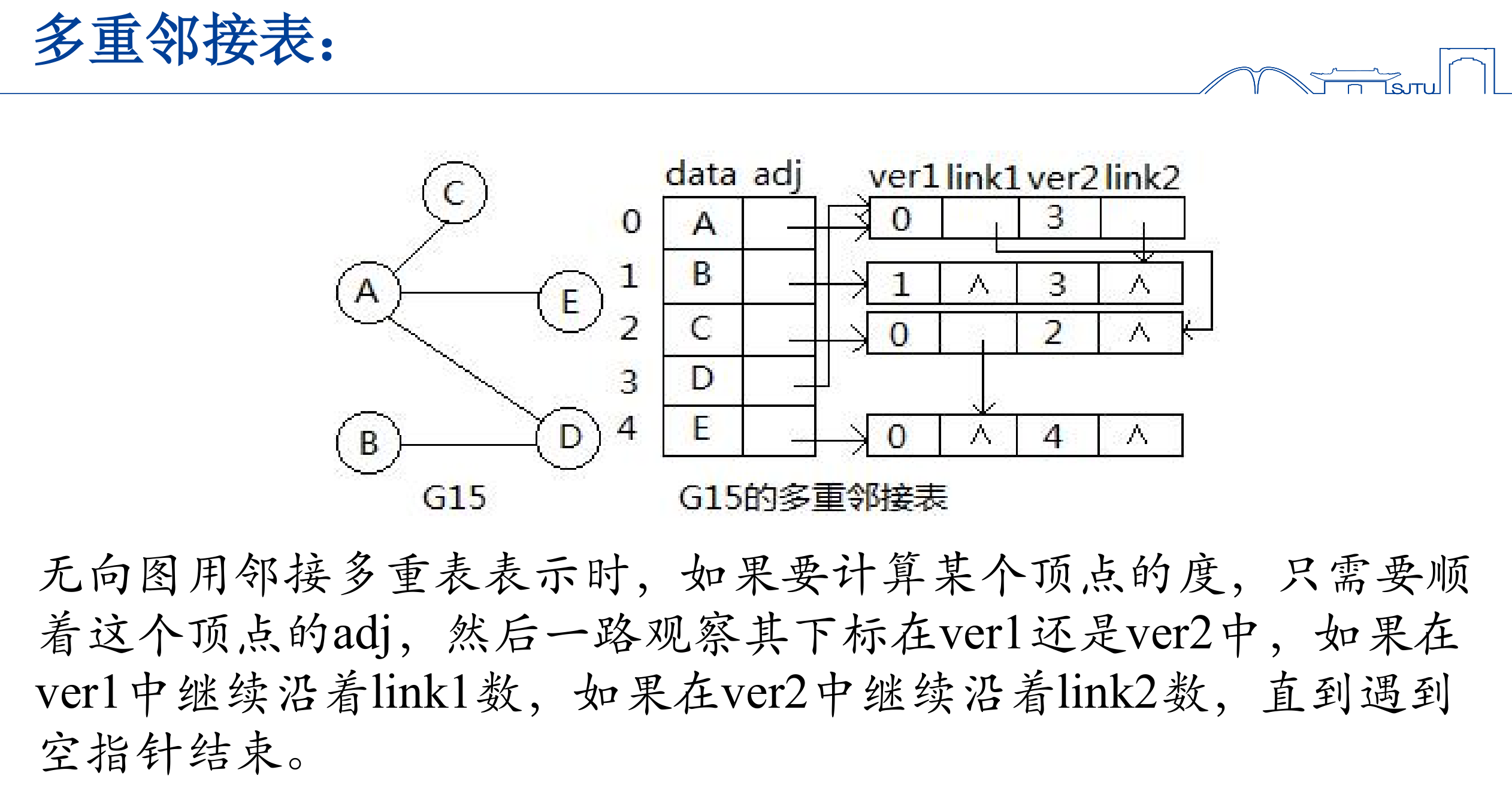
多重邻接表

对于无向图的邻接表，每一条表都对应的两次链接，存在空间浪费。

• 多重邻接表中每条边仅使用一个结点来表示，即只存储一次，但这个边结点同时要在它邻接的两个顶点的边表中被链接。
• 每一个边界点需要储存两个顶点$ver_1, ver_2$的信息，不妨假设$ver_1 < ver_2$

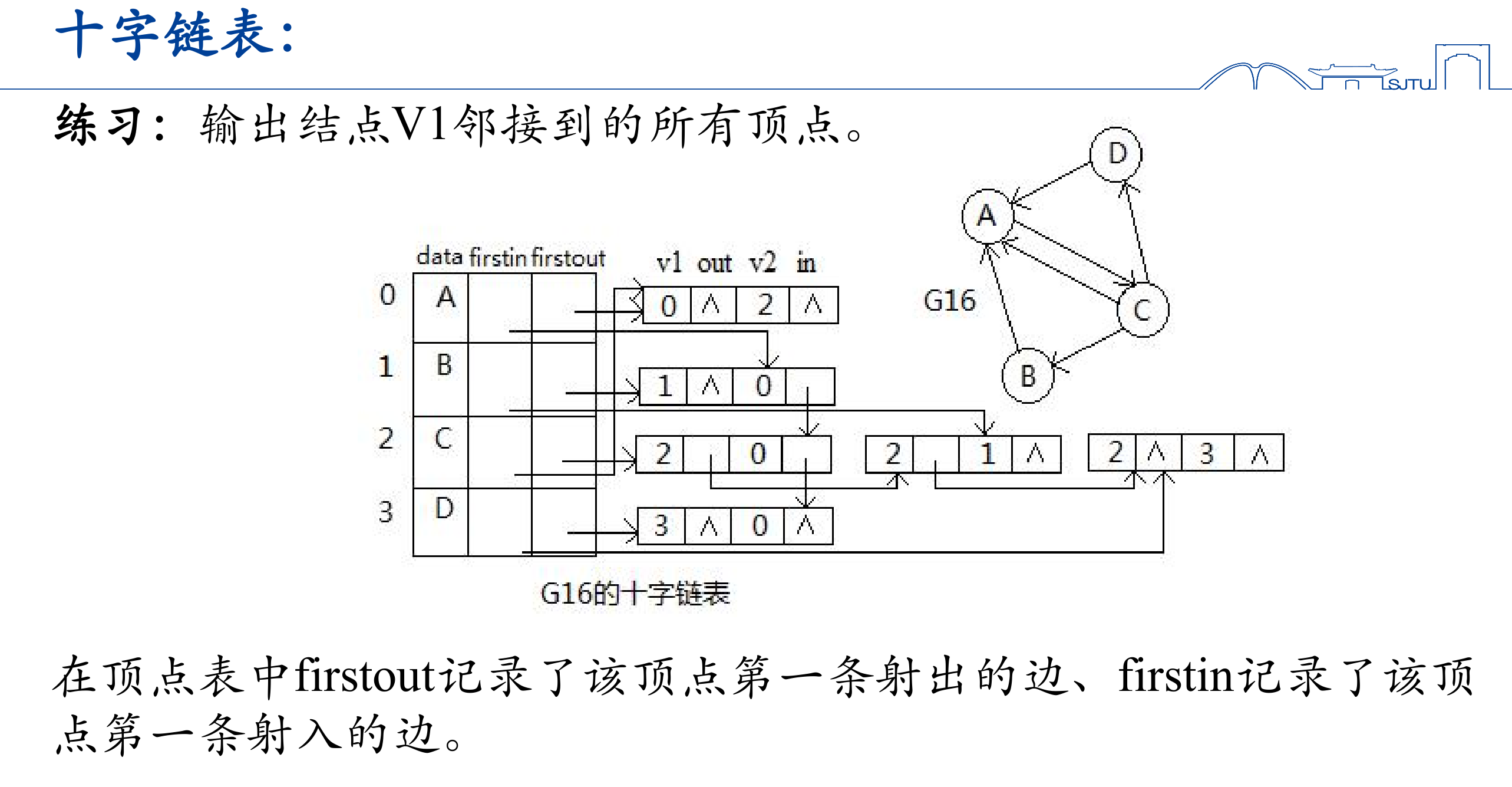
十字链表

如何将邻接表和逆邻接表结合在一起（同时方便的计算出度和入度），因此在数组中需要衍生出两条链表，一条代表出，另一条代表入。并且借鉴多重邻接表的思想，每一个节点直接模拟边的行为，并且对于有向图而言，需要区分in 和 out。

图的算法

• 图的遍历算法

  • DFS 和 BFS
    • 图的连通性
    • 欧拉回路算法

• 最小代价生成树算法

• 最短路径算法

• AOV网和AOE网

• 网络流问题 (Optional, to de done)