DataStructure Graph AOE and AOV Network
Introduction
在本文，我们将会介绍两种DFS算法的基本应用：AOV网络和AOE网络
AOV
我们假设一个工作流如下：
我们定义一个原子化任务为$T_k = \{ A_k, S_k \}$，其中$S_k \subseteq \bigcup \{T_i \}$代表前置任务的集合。
在访问$T_k$之前，需要满足以下的前提条件：
$$\forall x \in S_k(x \text{ is visited.})$$
AOV网是对现实工作的真实建模，不同的工作之间往往存在先后之分。例如，你需要在学习数据结构之前学习程序设计。
如何根据工作流建立数据结构？很显然，我们可以使用拓扑排序和深度优先搜索来实现！首先，我们需要保证图是有向无环图，因为我们需要建模的是不同节点之间的依赖关系。
建模之后示例如下：
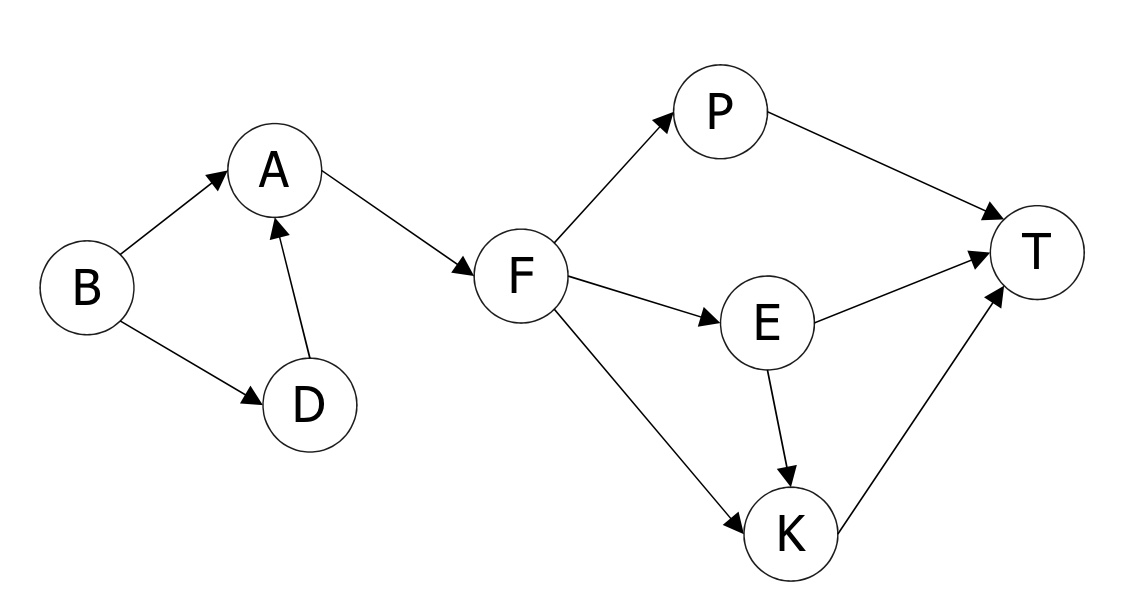
可以看到有向边代表的信息是不同节点之间的继承关系，而每个节点表示具体的原子任务，上文建模中的$S_k$就是对应节点的所有first endpoint组成的集合，也就是入度。因此，我们把这种网络叫做 Activity on Vertex Network (AOV Network).
拓扑排序
如何实现拓扑排序？
- 首先找到一个入度为0的点。
- 入度为0可以形象地概括为这个节点的全部预备先修节点已经被访问了，逻辑上的
- 从这个节点开始，访问该节点。
- 在逻辑上删除它和从它出发的所有边。
- 对它的后继检查入度是否为0。
- 如果其后继存在入度为0的点，继续push进入队列。
- 如果队列为空但是并没有遍历完全，说明节点存在环，不符合有向无环图的定义。
时间复杂度：$O(|V| + |E|)$
一般来说，线性的图论算法如果使用邻接表存储可以达到$O(|V| + |E|)$的时间复杂度，如果使用邻接矩阵存储可以达到$O(|V|^2)$的时间复杂度。
- 如果为稀疏图，$|V|$很大但是$|E|$很小，此时邻接矩阵会存在严重的空间浪费问题，因此使用邻接表储存更方便。
- 如果为稠密图，$|V|$很小但是$|E|$很大，那此时邻接表的存储是非常高效且简单的，反而邻接表的使用更加的复杂。
AOE
In contrast, we have Activity on Edge Network (AOE Network) as follows:
顾名思义，我们此时需要把活动定义在有向边上，而不是在节点上。
我们假设在一个工作流存在若干个时刻，$t_0,t_1, t_2, t_3, \cdots,t_n$.这里只考虑离散化的时刻。我们把第一个时间节点定义为源点($t_0$), 把最后一个时间节点定义为$t_n$，即汇点。
我们允许并行事件的发生
但是和AOV一样，事件之间存在严格的先后关系。
将活动定义在有向边上，而不是定义在节点上。
顶点代表事件，而有向边的权值代表某个活动的持续时间。有向边的方向代表事件先后的发生次序。
AOE网的关键：遍历所有节点的最长时间，以及那些节点事件是影响工程进度的关键事件。
因为我们允许时间并行，因此从源点到汇点的最长时间就是完成工程的最短时间。（当最长路径上的活动完成之后，其他路径长的活动肯定已经完成）
这貌似是一件很荒谬的事情，不过是正确的。
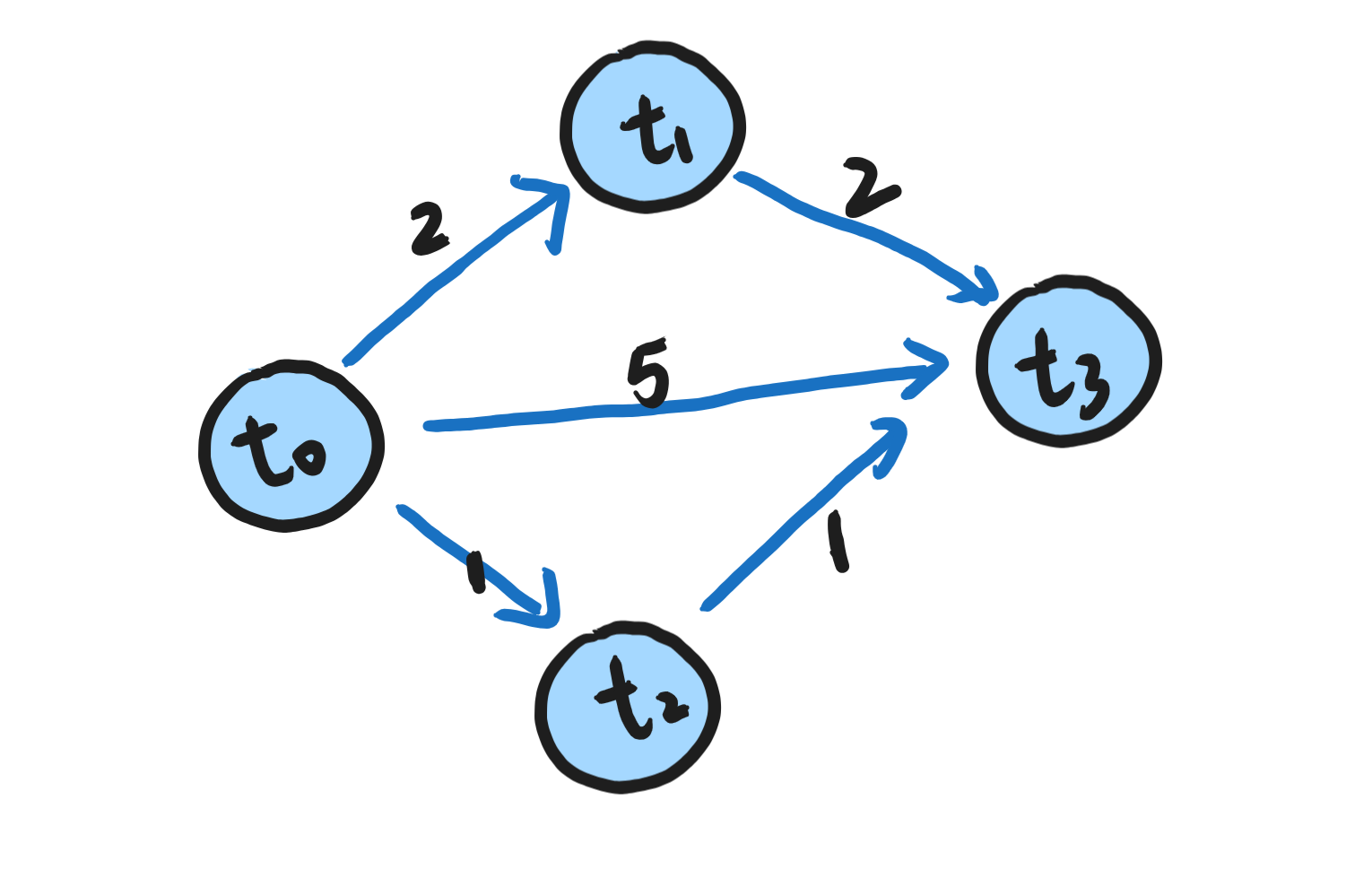
我们来看上面的图，把$t_0$作为源点，$t_3$作为汇点，我们的任务是要在尽可能的短的长度内遍历图上所有的点（允许并行）。
很显然，从起点到终点的最短路径长度为2，即走最下方的那条路。但是问题在于此时达到汇点之后需要等待上游两条路结束，此时我们的任务还没有完成。
我们可以理解为我们需要等最慢的支路完成了，此时才可以认为整体的支路完成了。
因此，我们就可以明确我们的目标：求从起点到终点最长的路径。
Given the starting point $x$ and the ending point $y$, we need to find the longest path from $x$ to $y$. (Practically, it means the worst situation of an event). We call it a critical event.
更新的算法也很简单，使用类似于动态规划的思想：
$ee(v_i) = \max \{ ee(v_k) + L_{k,i} \}$
使用一次DFS遍历，不断更新下一个节点的最长长度。
不过同时，我们还需要计算顶点的最迟发生时间，转化一下就是如果我们倒着看，就是从终点向起点的最长发生时间。（在我们已知收点的最迟发生时间的情况下），按照逆拓扑序的顺序找到最小值。
如果最早发生时间 == 最迟发生时间，说明这个节点很关键（被卡脖子了）。