DataStructure B and B Plus Tree

外部查找和排序

外部存储

我们考虑如下的数据单元：

template<class KEY, class OTHER>
struct set {
    KEY key = KEY();
    OTHER other = OTHER();
};

key储存的是关键字值，而other储存的是其他信息。这样一种数据储存的方式非常的常见，例如json文件，或者我们在建立一个人口数据库，对每个人会有一个身份证号（关键字值）和其他信息（Other）组成。

但是问题在于，计算机的内存是非常有限的，如今配置较高的笔记本内存也仅仅在32GB中，如果为了一个查找程序把所有的数据塞入内存中，很显然是不显示的，因此我们需要储存在外部。

储存在外部的代价是访问速度的大幅度下降，1秒钟，可以执行$25000000$条指令或进行$6$次磁盘访问。对于储存在外存的数据中，数据的性能瓶颈关键在于外存数据的访问，即磁盘的访问数据。因此，如果我们要实现外部数据的高效查找，首先需要实现的就是尽可能少的做磁盘读写。

如何解决？

如果我们还是使用树的结构，毋庸置疑我们需要降低树的高度，即一棵树储存的不止两个子节点，这样就可以降低树的高度，实现尽可能少的内存访问次数。但是这样还是存在一个问题：我如何保证树的平衡特性？

因此，我们介绍新的数据结构：B树。

B树

显然，我们不希望外存上的数据变成一颗二叉查找树，因为这样树的每一次访问都将举步维艰。

先来看一颗B树长什么样子：

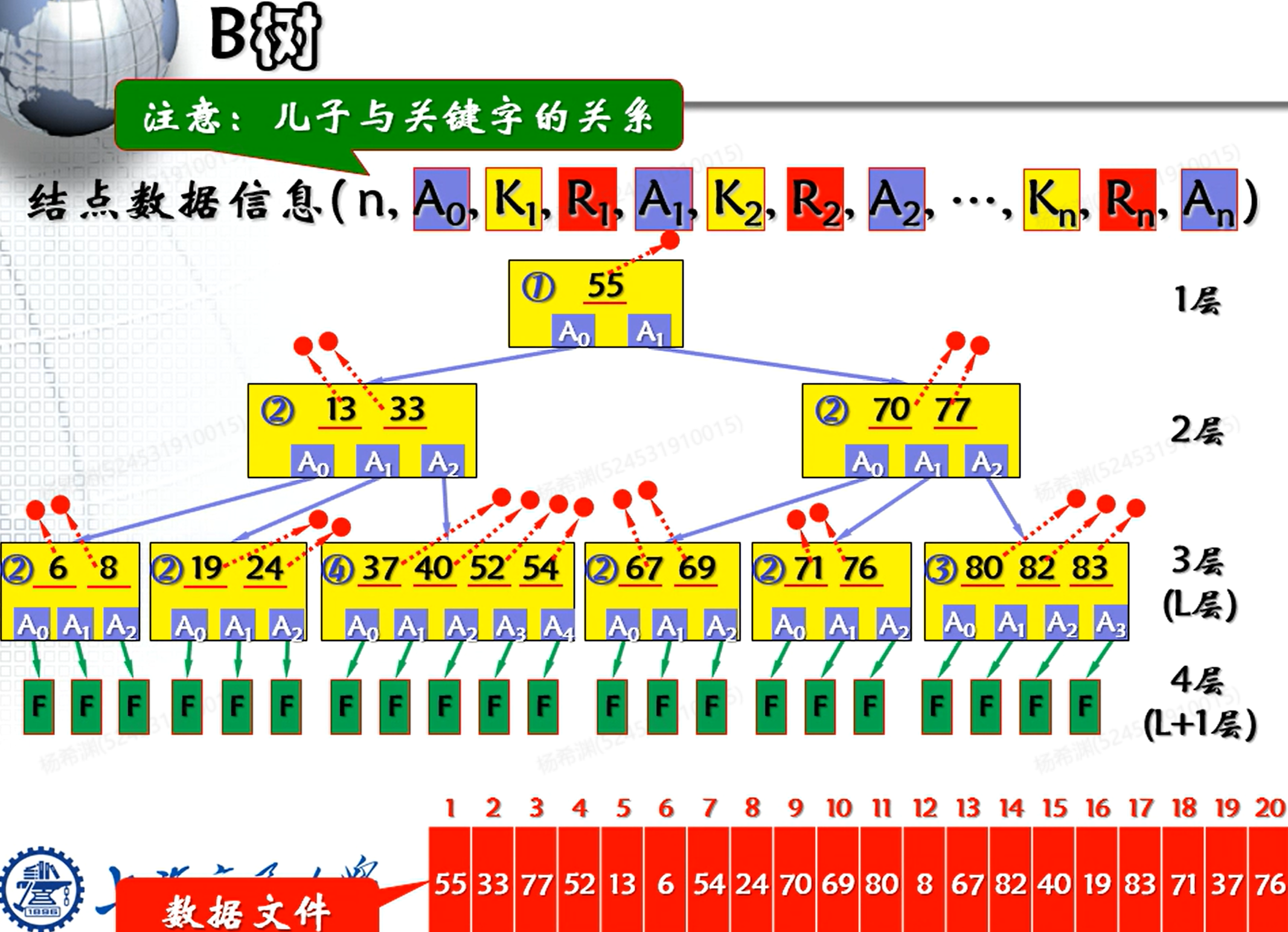
$n$代表每一个节点的关键字的个数。（此时这个节点就有$n + 1$个儿子节点）

右下角红色的就是按照顺序存储的在外存中的数据文件，我们在内存中储存了一个B树，对于每一次问询（给出一个关键字），我们都需要现在储存在内存中的B树中进行查询，在查询到对应元素在外存中的地址之后再去访问磁盘，即去访问外存中对应的数据。

在B树中，储存的都是数据元素的指针。

Definition

为了保证树的平衡性，B树需要再M岔树的基础之上额外添加一些定义的约束：

了解定义之后，再来看一眼B树：

同时，随着高度的增加，节点存储的关键字的个数增加，故可以保证树的高度是平衡的（这个被写进定义了）

$$h \le \frac{\log_{t}(n + 1)}{2} + 1$$

其中$t$为树的最小度数，n为含有的关键字的总数。

有关B树的定义非常的抽象，我们做一点注解：

• 每一个关键字可以看做是对后续节点做分化的隔板。
  • 这本质上还是一颗有序的查找树！
• 为什么B树会保证不会退化始终平衡？因为他简单粗暴的保证了每一个节点存在一个最小度数$\left \lceil \frac{m}{2} \right \rceil $。
• B树是为外存储器设计的，这里的节点是广义节点，每一个节点内部可以储存很多个关键字值的信息。在实际中，可以把一个磁盘块储存为一个B树的节点，根据磁盘块的物理参数来决定B树的阶数。

查找

B树的查找本质上和二叉查找树不存在差异：从根节点出发，比较关键字值和所储存的关键字值的位置。（应该插入到那个位置），然后走向对应的节点。因为B树的分支特别的多，因此会抛弃更多的分支，实现更少的访问外存的次数。

插入

查找树在插入的过程中都是插入到叶节点中，对于B树也是如此，只不过这里是指“最后一层的节点”而不是代表查找失败、不储存任何信息的叶节点。

判断节点是否有空位置：

• 有：新增加一个关键字。
• 没有：此时设计节点的分裂操作。

对于节点的分裂操作，可以看做如果当前节点在插入后存在$M$个关键字，我们需要将这个节点进行分裂：

• 对关键字值进行排序后切分：
  • $[1,mid-1]$，${mid}$，$[mid +1, right]$
  • 左右两个区间重现变成两个新的节点。
  • 中间元素？因为需要保证二叉树的定义，现在分裂后父亲节点的子节点数增加1，因此对应的父亲节点的关键字数要加1，因此这是一个不断向上访问的过程，直到访问的根节点，因此在最坏情况下我们可能需要让这棵树的整个元素+1！

删除

基本逻辑一样：先进行查询之后再寻找位于底层的替身元素。（其儿子节点中最小的值）

接着进行删除的操作：如果删除之后仍然满足二叉树的定义，直接删除关键字值（对应的索引）即可，否则需要调整。（我们需要保证度数不小于最小度数）

领养

领养父亲的一个关键字值，同时把兄弟的一个关键字值上提到父亲节点处。例如在这里删除$50$的关键字值，此时需要将父亲节点的53下放（领养）到儿子节点。

合并

如果相邻的兄弟节点囊中羞涩，无法给出空余的节点，那么这个时候就需要将父亲节点的一个关键字下移合并给兄弟节点。

同样的，和分裂节点类似，此时需要继续向上调整祖父节点。

同样，也有可能出现整棵树高度减少1的情况：

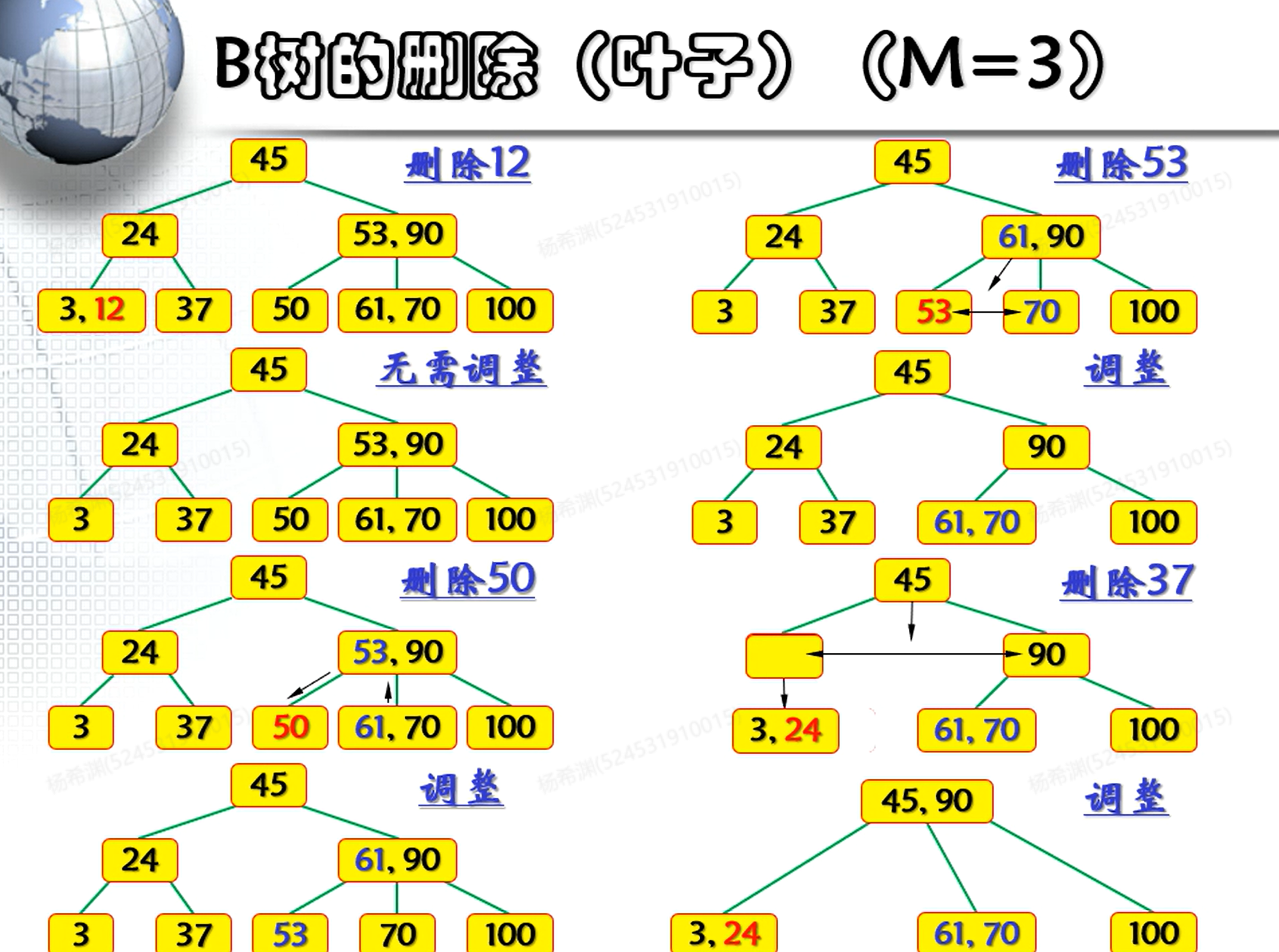
B树的特点

回顾B树的数据结构，我们发现B树本质上是对在外存上一段连续空间内存上数据建立了索引文件，并且按照关键字值的大小构建起了一颗二叉搜索树。

这样的结构设计对于单点搜索操作是非常方便的，因为树的分支因子较大，因此可以尽可能的减少树的高度，实现更少的磁盘访问次数。对于数据的删除和插入操作：

• 插入：在外存数据中append到末尾，并将索引项插入到B+树中。
• 删除：直接删除B+树的索引项即可，不可以挪动外存中其他位置的数据，不然索引会乱掉。

缺陷

但是B树的缺陷也非常明显，从插入操作中可以看出，B树并没有对外存数据的储存做过多的约束（就直接append到这个连续内存数组的末尾，也不会清理删除的数据），这样就会导致：外存数据储存中关键字的值是乱序排列的！也就是说，B树实现顺序遍历的时间复杂度是灾难性的，因为他需要中序遍历一整颗树然后做$N$次单点操作。

我们继续介绍B+树来弥补这个漏洞。

B+树

索引数据文件：即支持对单个数据的访问 又支持对这个文件按关键字的次序进行顺序访问。

B树建立了一个索引树（索引文件），可以支持快速查找某个记录，但是无法实现对磁盘的顺序访问，因此无法被称作索引数据文件，关键就在于数据是储存在外存的一个一段连续数组上的，而B树仅储存对应值的索引。

我们在B树的基础上可以得到B+树，实现顺序访问。

Chunking

我们期望B+树可以达到：

• 和B树时间复杂度相当的单点操作
• 可以实现按照关键字值对外存数据顺序遍历
• 插入 & 删除等操作的时间复杂度也应该和B树相当

我们自然会想到使用链表来储存外存中的数据，如果使用普通链表，时间效率会很低（随着$N$的不断增大），因此我们需要使用块状链表即分块的思想来实现这个数据结构。

Definition

B+树的设计和B树略有不同：

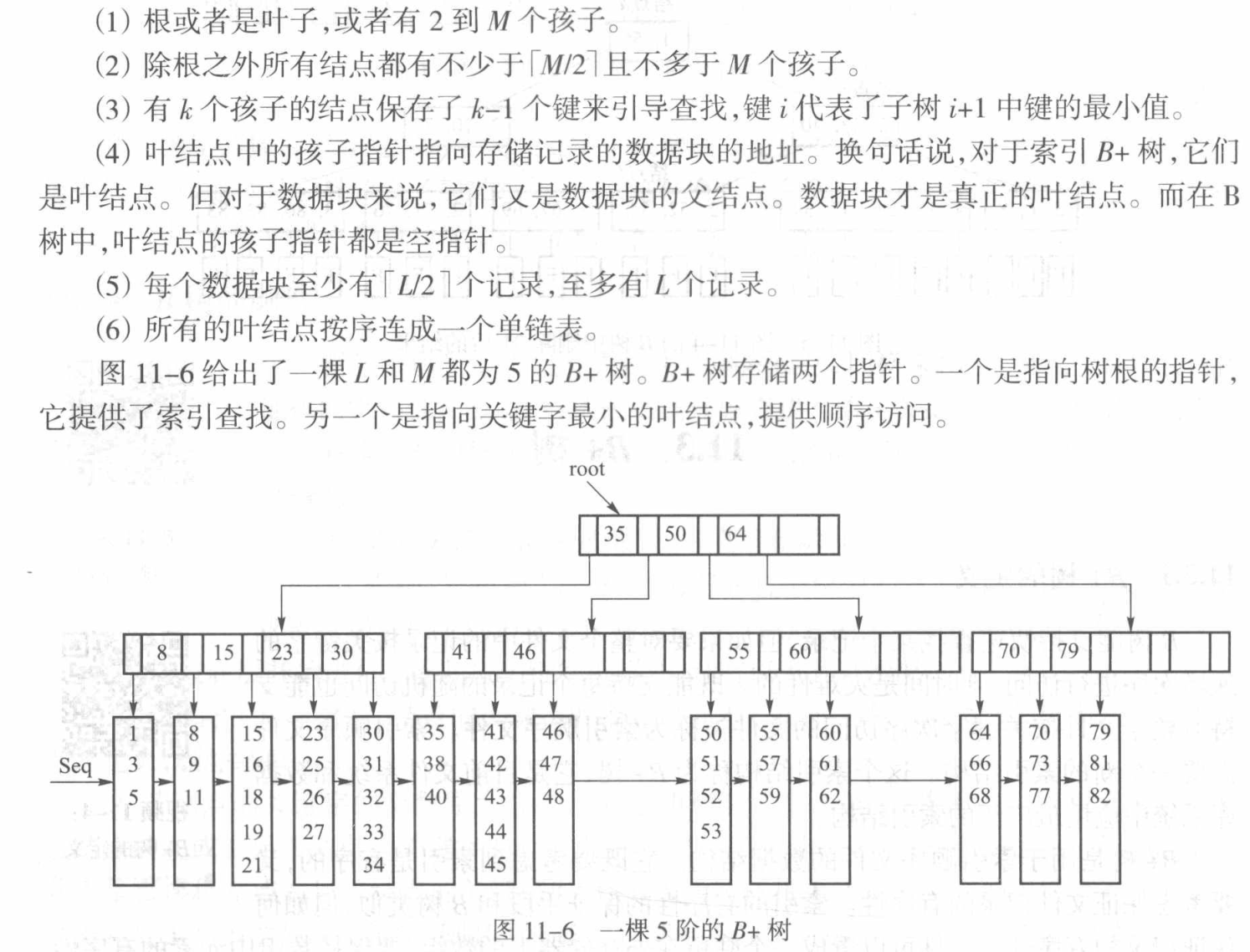
一些不同的地方：

• B+树直接将数据储存在叶子结点上（分块的思想）
• 对于每一个分块储存的数据元素的数量也有$\left \lceil \frac{L}{2} \right \rceil \le x \le L $的限制，保证平衡。
• 为了支持顺序访问，块内部和外部都必须保证有序。

其他关于索引树的节点的定义和B树类似，不做重复介绍。

Insert

和B树的操作类似，首先需要查找数据块知道叶子结点（数据节点的上一层）。

• 将新的数据插入对应的叶子（保证块外部的有序），并对块内部的元素顺序进行调整（保证块内部的有序）
• 如果出现非法情况：
  • 需要被插入的块已经满员了，需要做节点的分裂操作。
  • 如果当前节点还有空位（$n \le M$），即生成一个新的关键字储存在当前节点中（因为多了一个儿子）
  • 如果没有空位了（$n = M, n + 1 > M$）,此时需要继续分裂，并且继续向上更新父亲节点

例如，在当前的树中插入22：

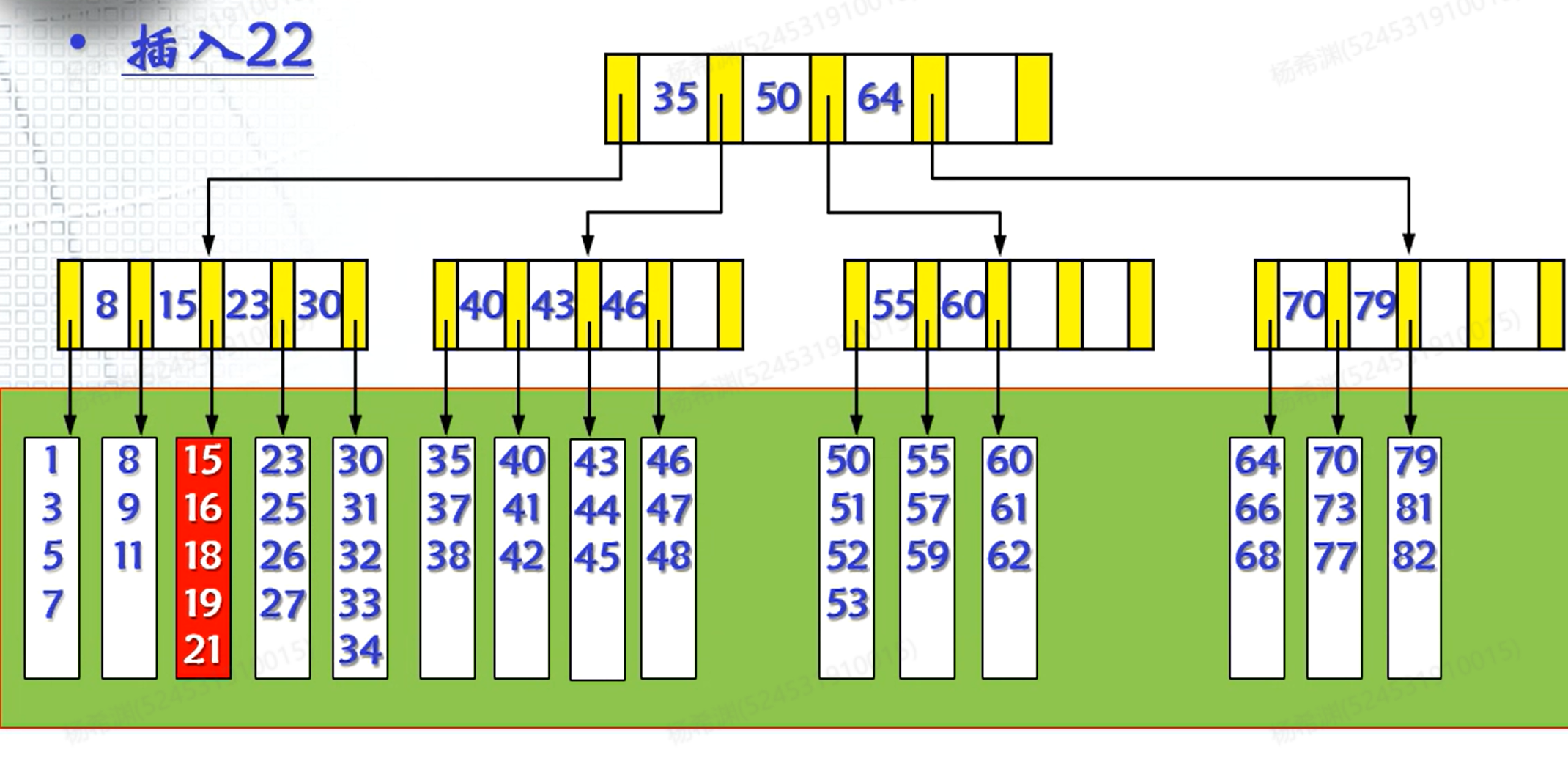
在这里发现插入之后满员了，分裂节点发现也没有办法容纳新的儿子，于是分裂上一层的节点。

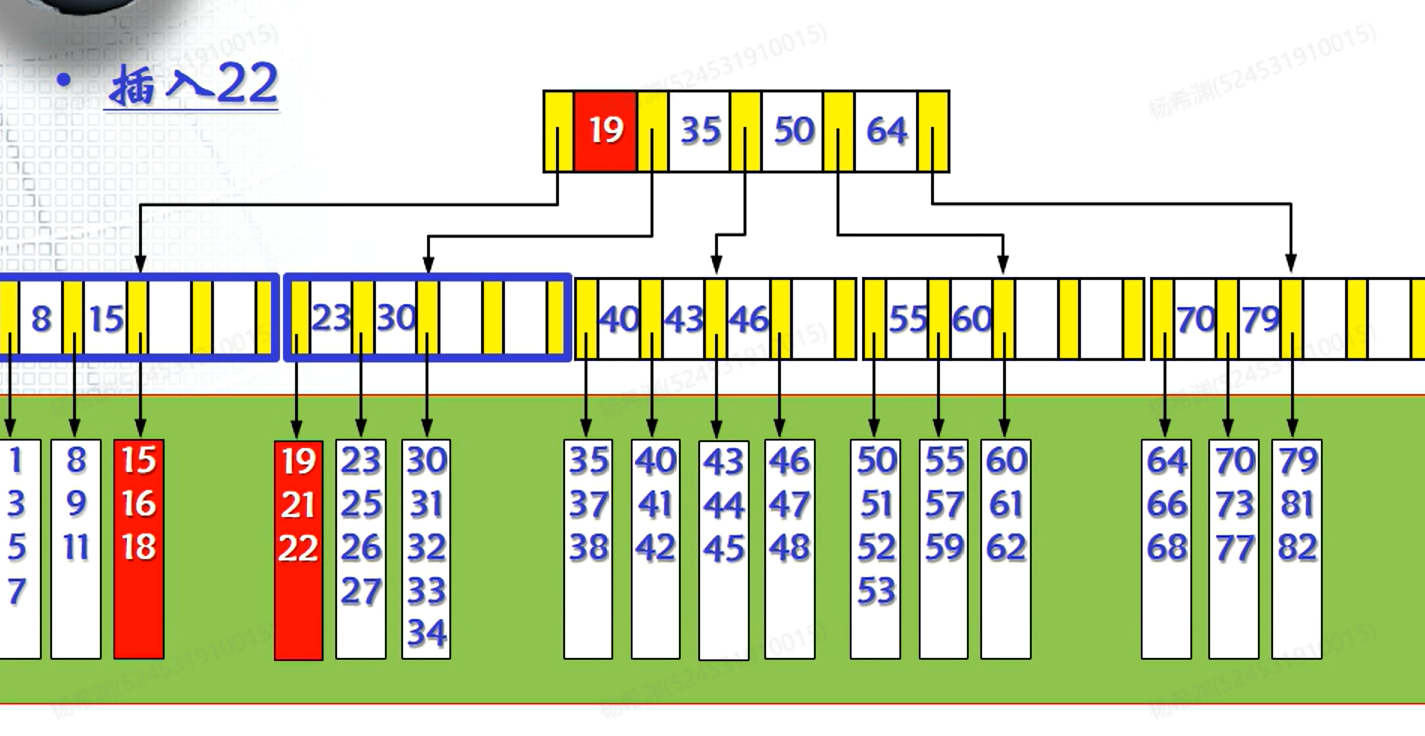
Deletion

和B树非常类似，首先在对应的叶节点数据块删除对应的数据。如果满足定义就不作操作。（保证有序就可以）

• 如果删除元素导致某个块的数量不足$\left \lceil \frac{L}{2} \right \rceil$，需要调整树的结构。（唯一可能出错的情况）

首先想到的是领养操作，即看左右的邻居节点，如果没办法领养，就需要合并邻居节点。

继续，此时父亲节点的儿子数和关键字树不匹配，父亲节点需要删除一个关键字值，继续向上过滤作删除操作。

M和L的选择

外存读写的单位为块，一个块存放一个节点能使IO效率最高。对于一个$M$阶B+树来说：

$$(M - 1)\times 32 + M \times 4 \le 8192$$

$$M \le 228$$

• 32是关键字值的字节数（例如int或者size_t）
• 4代表分支的字节数（储存地址）
• $8192$是单个磁盘块的大小

$L$的选择和数据块的大小有关，通常$L = 32$（假设每一条数据记录256个字节）

复杂度分析

最坏情况下，所有节点都在下界，即有$\left \lceil \frac{2N}{L} \right \rceil $个叶节点。

树的最高深度 $\log_{\left \lceil \frac{M}{2}\right \rceil}(\left \lceil \frac{2N}{L} \right \rceil )$

我们取$M = 228$，此时M是非常大的，树的层数就很低，把磁盘的访问次数下降到最低。（包括插入 & 删除 & 归并等等操作）

对于最坏的情况，分裂和归并到顶层，可能会导致树的高度升高1或者下降1，但是均摊来看还是很高效的复杂度。

Additional

B*树

B*树是在B+树基础上的进一步优化，在 B+ 树的非根和非叶子节点再增加指向兄弟的指针：

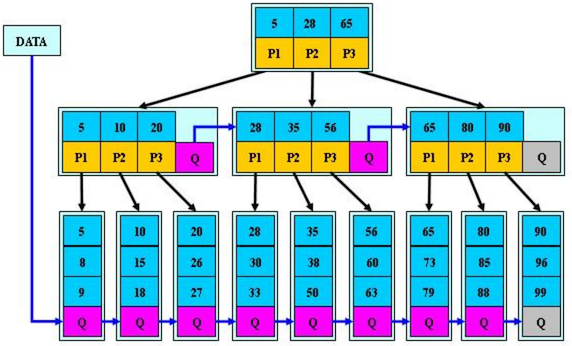
• B*树要求非根节点至少2/3满(约66.7%)，提高了空间利用率

• 当节点满时，B*树不是立即分裂，而是尝试将部分键值重新分配到兄弟节点（使用链表链接，可以“转移”）

• 只有当两个相邻兄弟节点都已满时，才会将这三个节点分裂为两个

• 这种策略减少了分裂频率，提高了空间利用率

R树

R树是为空间数据(如地理坐标、多边形等)设计的索引结构，与B+树家族有显著不同：

1. 空间索引能力：
   • B+树只能索引一维数据
   • R树可以高效索引多维数据(如二维坐标、三维空间数据)
2. **基于最小边界矩形(MBR)**：
   • 每个节点存储的是空间对象的最小边界矩形
   • 允许快速过滤不相关的空间查询
3. 查询类型支持：
   • 支持空间查询如”查找附近的所有点”
   • 支持范围查询如”查找这个矩形区域内的所有对象”
   • 支持最近邻查询
4. 变体改进：
   • R+树：避免节点覆盖区域的重叠，提高查询效率
   • R*树：通过优化插入、分裂策略和强制重新插入来提高性能
   • Hilbert R树：使用空间填充曲线对对象排序，改善结构

R树的关键在于对点做分类，并以此建立MBR，然后一层层向上建树，知道囊括数据中的所有点。

怎么一股线段树的味道。

外排序

显而易见，外排序就是对储存在外部储存器上数据进行的排序。以磁带储存器为例，其为顺序存储设备，完成有效的排序至少需要两个磁盘机，当然，多多益善。

三个磁盘机可以实现轮转的排序（并行的思想）

外排序主要考虑减少外存储器的读写次数，和内排序的时间瓶颈不同。

外排序的基本方法

• 预处理：分成有序片段（读入内存之后使用内排序）
• 归并：把有序片段归并成一个有序文件
  • 多路归并
  • 多阶段归并

预处理：置换选择

把外存的数据读入内存进行内排序的时候，我们希望每一个排序片段的size尽可能的大（即排序片段的数量尽可能的少），这样就可以使归并的次数尽可能的少，因为每一次归并操作都需要线性扫描两个待归并的序列，如果归并次数过多，意味着存在重复被扫描的元素。

我们介绍置换选择法，可以在$p$的内存空间中实现平均长度$2p$的序列排序，这比最笨的一段一段排序要快很多。

• 在初始状态下，读入size为$p$的序列，进行内排序（保证有序性），输出最小值。
• 这个时候内存存在空间剩余（这是我们需要利用的地方！），我们可以再读入一个值，并调整这个值所在的位置，维持有序性。

在这里内排序的时间开销远小于外排序，因此可以忽略这一点小小的优化。

我们既输出的值为$x_o$，输入的值为$x_i$：

• $x_o < x_i$：说明如果$x_i$参与这一次排序的话，他的位置肯定在$x_o$的后面（还有机会！），因此作为新元素被插入，参与排序
• $x_i < x_o$：没有机会，$x_i$不会参与这一次排序，但是可以一直占着坑，自动进入下一次排序。

归并

多路归并

我们首先介绍两路归并：$k = 2$

两路归并需要四条磁带的使用：$A_1, A_2, B_1, B_2$，每两条作为一组，两根作为输入，两根作为输出。

• 轮流将已被排序的片段写到$A_1, A_2$两条磁带上。
• 取$A_1$, $A_2$上各一个片段，进行归并操作，生成的新片段写入$B_1$。
• 再将$A_1$, $A_2$上剩下的片段转移到$B_1, B_2$上，在同样的做类似的操作。

一般地，对于$k$路归并，我们需要$2k$条磁带做运算，并且我们需要维护一个堆来找到最小的元素。

多阶段归并

使用多阶段归并可以实现$k + 1$条磁带的$k$路归并。