CS294-1-LLM-Reasoning
CS294/194-196 Large Language Model Agents
Introduction
In this course, you will learn several basic concepts of LLM reasoning and build agents based on LLMs. This course map are shown as follows:


Lec1: LLM reasoning
Intermediate Steps works

Reasoning: Humans can learn from a few or even no examples during the process because humans can reason! Traditional ML methods fails: Auto-encoder, require vast amount of labeled data.
Training LLMs needs a new way (few-shot or zero-shot prompting).
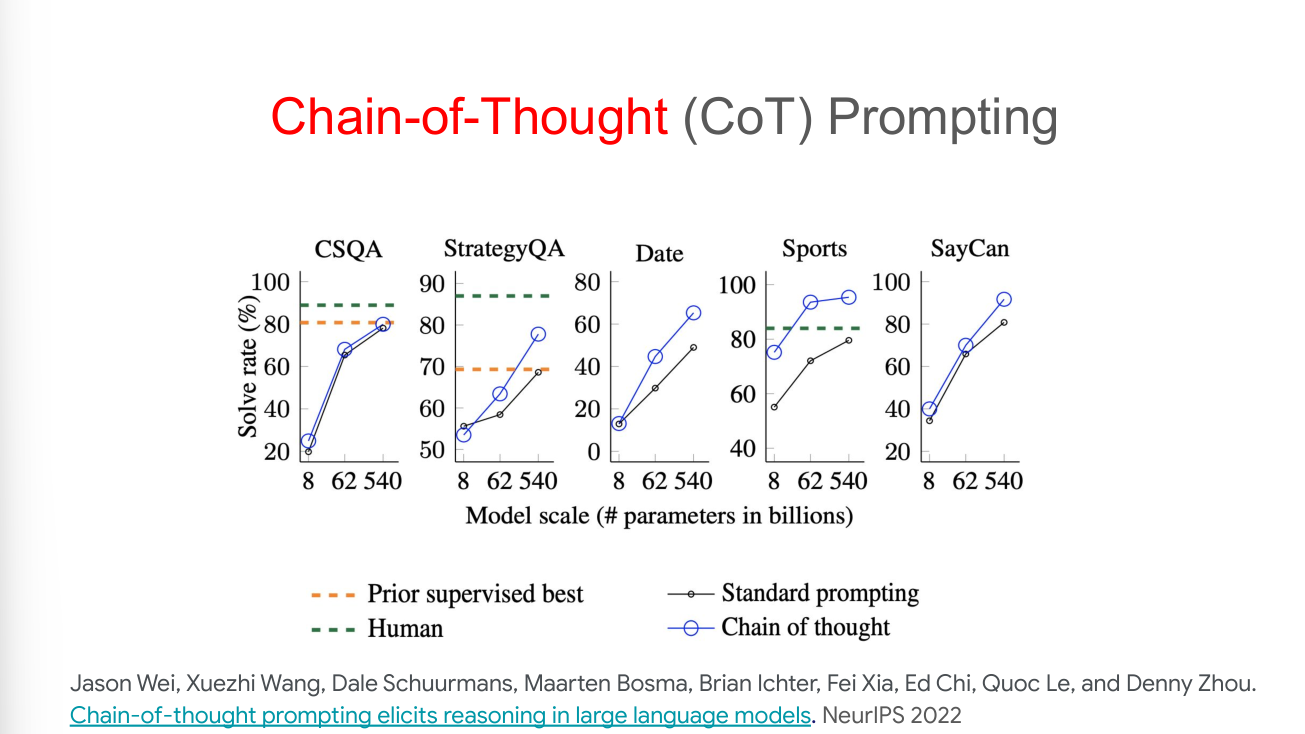
So how to make LLMs implement this? Let’s think step by step! Paper1[1] shown below in ACL 2017 first shows the effectiveness of introducing intermediate steps when designing model’s architecture. Following the work by Ling et al 2017, Cobbe et al 2021 in OpenAI built a much larger math word problem dataset (GSM8K) with natural language rationales, and used it to finetune GPT3.
How to implement intermediate steps? It’s the Chain-of-Thought! This is the foundation of modern mainstream reasoning models.
Regardless of training, fine-tuning, or prompting, when provided with examples that include intermediate steps, LLMs will respond with intermediate steps.
How to understand this? In my opinion, traditional machine learning methods, in simple terms, means finding patterns of labeled data points in a high-dimensional data space. This is essentially a process of finding patterns. Sometimes LLMs don’t provide the answer you want is for the reason of catching the wrong patterns. Providing intermediate steps enables LLMs to catch the right pattern more easily with the guidance.
This doesn’t end! We can make LLMs more powerful by training LLM’s reasoning abilities. In the book “How to Solve It”, the writer introduces decomposing and recombining are important operations of the mind. You decompose the whole into its parts and recombine the parts in a more or less whole.
We can simulate this process in LLMs, by enabling LLMs to think step by step on its own! In other words, LLMs can autonomously generate and decompose the whole problem and solve each sub-questions step by step.
In SCAN (Compositional Generalization) and CFQ (Text-to-code) tasks, this method uses just 0.1% demonstration examples and achieves perfect generalization. Moreover, we can make LLMs perform well without using demonstration examples, which is known as zero-shot prompting.
Analogical Reasoning
Analogical reasoning is an important think pattern that human solve new problem. When humans encounter new and difficult tasks, people tend to relate this problem to previously seen problems to get several ideas. That is experience. We also want LLMs to learn this ability.
“A mathematician is a person who can find analogies between theorems; a better mathematician is one who can see analogies between proofs and the best mathematician can notice analogies between theories. One can imagine that the ultimate mathematician is one who can see analogies between analogies.”
----Stefan Banach
Whatever the method is, we ultimately want LLMs to learn and comprehend the problem itself, rather than just wandering set on the basis of the limited data.
LLM reasoning without prompting
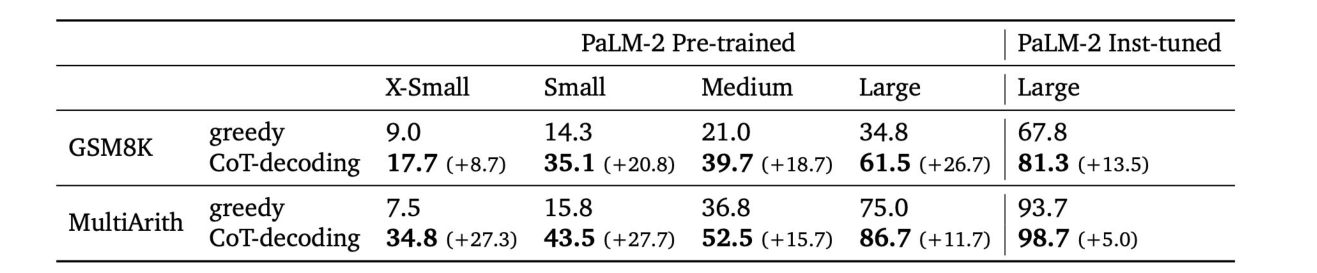
In previous research, zero-shot prompting perform worse than few-shot prompting. We can achieve LLM reasoning without prompting! Pre-trained LLMs, without further finetuning, has been ready for step-by-step reasoning, but we need a non-greedy decoding strategy to elicit it.
When a step-by-step reasoning path is present, LLMs have much higher confidence in decoding the final answer than direct-answer decoding.
In the graph shown as follows, CoT decoding performs better than greedy decoding.
Self-consistency
Limitations
Papers
This section is for several papers this course has recommended, some of which are demonstrated on the PowerPoint. By diving deeper into these lectures and slides again, you can absolutely gain a deeper meaning of LLM reasoning!
Paper1_Derive the Final Answer through Intermediate Steps
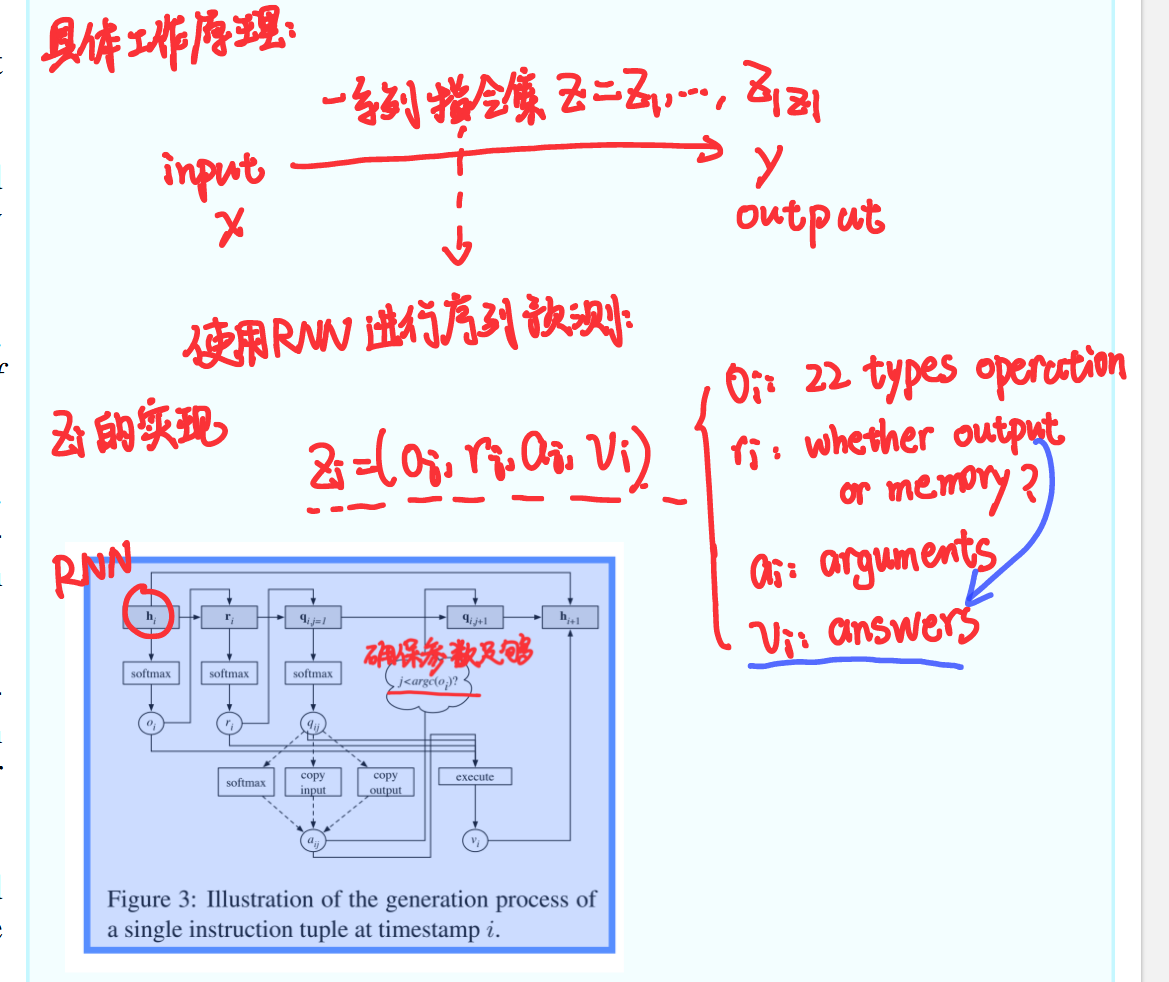
This paper[1] focuses on solving algebraic word problems by generating answer rationales. A new dataset with 100,000 samples of questions, answers, and rationales is created. The model proposed is a sequence-to-sequence model that generates a program’s instructions to produce the rationale and then the answer. It defines 22 operations and models each instruction based on the text program specification and history. Inducing programs is achieved by leveraging the progression in rationales and filtering possible instructions. Staged back-propagation is used to handle the memory challenge caused by long rationales. Experiments show that compared with baseline models like the attention-based sequence-to-sequence model with copy mechanisms, this model performs better in terms of perplexity, BLEU score, and accuracy. It demonstrates the effectiveness of using rationales to guide program induction in solving math problems and provides a new approach and dataset for future research in this area.
The model seems to have the reasoning ability, but actually its basic structure is still LSTM model (a version of RNN). Decompose the problem into smaller subproblems, ultimately transforming it into a series of instruction sets, making it difficult to solve more challenging mathematical problems. Moreover, transformer structure hasn’t been invented yet. But it proves the potential of generating intermediate steps while getting the final answer to decrease perplexity and enhance error rate.
References
The cite format is informal, the references below just list the url link of all papers.