Algorithm-Sorting

Sorting Algorithms

此处所有的排序算法都使用0-based。

Introduction

如何评价一个排序的好与坏？

排序的复杂度
- 时间复杂度：对数组排序所需要的时间开销。（最坏 & 平均）
- 空间复杂度：对应复杂排序函数的设计，往往需要额外的空间开销。
排序的稳定性：
- 稳定排序：对于关键字相同的元素的顺序不会变。
- 不稳定排序
排序的存储特性：
- 内排序：储存在内存
- 外排序：储存在外存

由于外存的设计导致其读取速度非常慢，我们放在下一章节《B和B+树》中详细讨论。今天讨论的排序算法都是针对在内存上连续空间的讨论。

根据排序的方式，我们主要可以分为以下的若干排序方式：

插入排序
- 直接插入排序
- 二分插入排序
- 希尔排序
选择排序
- 直接选择排序
- 堆排序
交换排序
- 冒泡排序
- 快速排序
归并排序
基数排序（桶排序）

Insert Sort

直接插入排序

类似于打扑克牌的插入过程，保持数组的有序性并不断在对应位置插入新的元素。

时间复杂度：$O(N^2)$ （逆序是最坏的情况）

Code

// Simple insertion sort
template<class Key, class Other>
void simpleInsertSort(set<Key, Other> *a, int size) {
    int k;
    set<Key, Other> tmp;

    // Start sorting
    for (int i = 1; i < size; i++) {
        tmp = a[i];
        for (k = i - 1; k >= 0 && tmp.key < a[k].key; --k) {
            a[k + 1] = a[k];
        }
        a[k + 1] = tmp;
    }
}

插入排序在原地移动就可以了，不需要使用额外的空间，对于外层循环，$[0,size)$代表已经被排序好的区间，并对$size$位的元素做插入操作。

复杂度分析

如果直接从代码角度分析，两个for循环嵌套直接$O(N^2)$，或者我们可以把这个过程abstract成若干个子过程：

找到需要被插入的位置。
执行插入操作。

二分插入排序

因为已排序的数组保证了有序性，因此可以在查找的过程中使用二分查找，比较的时间复杂度降为$O(N \log N)$，但是插入的时候时间复杂度没有下降，总的时间复杂度还是$O(N^2)$

希尔排序

Intuition：避免大量的数据移动，使用交换来替代大批量的数据移动。

先比较离的远的元素（此时步长大，移动的效率高）
步长不断减小直到1

在直接插入排序的过程中，每插入一个新元素都需要进行线性的移动才可以插入到正确的位置，希尔排序的关键在于减少排序移动的次数，因此希尔排序从步长大的开始，交换元素（相当于做了很多次的移动）。希尔排序选择了一个序列$h_1, h_2, h_3, h_4,\dots, h_t$，作为每一次的步长。

希尔排序的重要性质：一个$h_k-$有序的数组经过$h_{k-1}-$排序后仍然是$h_k-$有序，因此步长不断减小的排序逻辑是行之有效的！

最终希尔排序会执行一个$h_t = 1$的直接插入排序，看似时间复杂度不增反降，实际上，每一次排序都会接近于最好的情况，出现最坏情况的几率会少的多。

因此，希尔排序的关键在于希尔序列的设计，在这里我们选择了不断二分的希尔序列。

template<class Key, class Other>
void shellSort(set<Key, Other> *a, int size) {
    int step, i, j;
    set<Key, Other> tmp;

    for (step = size / 2; step > 0; step /= 2) {
        // shell array, finally is 1
        // do insert sort with stepsize of step
        for (i = step; i < size; i++) {
            tmp = a[i];
            for (j = i - step; j >= 0 && a[j].key > tmp.key; j -= step) {
                a[j + step] = a[j];
            }
            a[j + step] = tmp;
        }
    }
}

Select Sort

选择排序：对于元素中不断取出最小的元素（或者最大的元素），与数组的未排序的部分的首元素交换，实现序列的重组。

Simple Select Sort

对于直接的选择排序，对于未排序的部分（一开始就是整个数组），找出元素中最小的值，和第一个元素的值做交换。接下来未排序的部分就成了$a[2] \to a[n]$，接下来在做相同的操作。知道不存在未排序的部分。时间复杂度为$O(n)$，因为每次都要线性扫描未排序的部分来找到最大值或者最小值。

直接选择排序是一种稳定排序。

template<class Key, class Other>
void selectSort(set<Key, Other> *a, int size) {
    for (int i = 0; i < size - 1; i++) {
        int min = i;
        for (int j = i + 1; j < size; j++) {
            // the unsorted array
            if (a[j].key < a[min].key) {
                // find the minimum element
                min = j;
            }
        }
        std::swap(a[i], a[min]);
    }
}

Heap Sort

The basic principle of Heap sort is from the data structure: Heap, where all nodes (or elements) are formed in order (ascending or descending). Heap maintain this properties, so every time you pop out the top element in the heap (or priority queue), it must be the biggest or the smallest element with highest priority in the queue.

For more information, you can search Binary Heap

We can use several ways to construct a heap (Binary heap, leftist heap, skew heap, binomial heap), the code demonstrated below shows the basic implementation of Binary Heap:

#include <iostream>
#include <cstdlib>
#include <ctime>

template <class T>
class priorityQueue {
private:
    size_t currentsize;
    T* array;
    size_t maxsize;

    void doublespace() {
        T* tmp = array;
        maxsize *= 2;
        array = new T[maxsize];
        for (size_t i = 0; i <= currentsize; ++i) {
            array[i] = tmp[i];
        }
        delete[] tmp;
    }

    void buildheap() {
        for (size_t i = currentsize / 2; i >= 1; --i) {
            percolateDown(i);
        }
    }

    void percolateDown(size_t hole) {
        size_t child = 0;
        T tmp = array[hole];

        while (hole * 2 <= currentsize) {
            child = hole * 2;
            if (child < currentsize && array[child + 1] < array[child]) {
                ++child;
            }

            if (array[child] < tmp) {
                array[hole] = array[child];
                hole = child;
            } else {
                break;
            }
        }
        array[hole] = tmp;
    }

public:
    priorityQueue(size_t capacity = 100) : currentsize(0), maxsize(capacity) {
        array = new T[maxsize];
    }

    ~priorityQueue() {
        delete[] array;
    }

    priorityQueue(const T* data, size_t size) : currentsize(size), maxsize(size + 10) {
        array = new T[maxsize];
        for (size_t i = 0; i < size; ++i) {
            array[i + 1] = data[i];
        }
        buildheap();
    }

    bool empty() const {
        return currentsize == 0;
    }

    void enQueue(const T& x) {
        if (currentsize == maxsize - 1) {
            doublespace();
        }

        size_t hole = ++currentsize;
        while (hole > 1 && x < array[hole / 2]) {
            array[hole] = array[hole / 2];
            hole /= 2;
        }
        array[hole] = x;
    }

    T deQueue() {
        if (empty()) {
            throw std::underflow_error("Priority queue is empty");
        }

        T minItem = array[1];
        array[1] = array[currentsize--];
        percolateDown(1);
        return minItem;
    }

    T getHead() const {
        if (empty()) {
            throw std::underflow_error("Priority queue is empty");
        }
        return array[1];
    }
};

template <typename T>
void pqsort(T* unsorted, T* sorted, size_t size) {
    priorityQueue<T> pq(unsorted, size);
    for (size_t i = 0; i < size; ++i) {
        sorted[i] = pq.deQueue();
    }
}

template <typename T>
void heapSort(T*& arr, size_t size) {
    //default for ascending order
    priorityQueue<T> pq(arr, size);
    T* sorted = new T [size];
    for(size_t i = 0; i < size; ++i) {
        sorted[i] = pq.deQueue();
    }
    delete[] arr;
    arr = sorted;
}

int main() {
    int size = 50;
    int *arr = new int [size];
    
    //using the random seed
    std::srand(static_cast<int>(std::time(nullptr)));
    for(int i = 0; i < size; i++){
        arr[i] = std::rand();
    }

    std::cout << "Before the sort" << std::endl;

    for(int i = 0; i < size; i++){
        std::cout << arr[i] << std::endl;
    }

    heapSort(arr, size);

    std::cout << "After the sort" << std::endl;
    for(int i = 0; i < size; ++i){
        std::cout << arr[i] << std::endl;
    }
    return 0;
}

当然，我们也可以直接使用STL中的堆来实现这一操作：

template<class Key, class Other>
void heapSort(set<Key, Other> *a, int size) {
    // Use a custom comparator for a min-heap
    auto cmp = [](const set<Key, Other> &lhs, const set<Key, Other> &rhs) {
        return lhs.key > rhs.key;// Min-heap: smaller key has higher priority
    };

    std::priority_queue<set<Key, Other>, std::vector<set<Key, Other>>, decltype(cmp)> pq(cmp);

    // Build the heap
    for (int i = 0; i < size; i++) {
        pq.push(a[i]);
    }

    // Extract elements from the heap in sorted order
    for (int i = 0; i < size; i++) {
        a[i] = pq.top();
        pq.pop();
    }
}

注意自定义比较函数的设计！

可否优化？

在时间上，建堆的时间复杂度为$O(N)$，每一次出堆的时间复杂度为$O(\log N)$，因此总的时间复杂度为$O(N \log N)$。

时间复杂度赏心悦目，但是引入了额外的空间开销：我们有$O(N)$的空间复杂度来维护一个堆。针对堆排序，我们是否可以借鉴堆的思想但是实现$O(1)$的空间复杂度呢？Of course you can!

为了实现空间复杂度的压缩，我们需要：

原地建堆。
随着堆元素的减少将被删除的元素append到元素的末尾。

有关具体的代码实现和二叉堆的实现非常类似（使用顺序存储满二叉树），我们将只会使用函数percolateDown()函数，在建树的时候正常对每一个非叶结点做过滤操作，然后在删除的时候我们并不是实质上的删除元素。（我们甚至都没有建立一个堆！）我们只是实现元素的交换顺序。

template<class Key, class Other>
void OwnHeapSort(set<Key, Other> *a, int size) {
    for (int i = size / 2 - 1; i >= 0; i--) {
        // build for all nodes
        percolateDown(a, i, size);
    }

    // dequeue
    /*
    i is the size of the current heap
    std::swap(a[0], a[i]) means pop the first element of the heap (swap with the ith element at the back)
    then use percolatedown to make the heap sorted again.(Use for a[0] only)
    */
    for (int i = size - 1; i > 0; i--) {
        std::swap(a[0], a[i]);
        percolateDown(a, 0, i);
    }
}

/**
 * @brief percolate down for the heap sort
 * 
 * @tparam Key 
 * @tparam Other 
 * @param a the array to be sorted
 * @param hole the starting position of percolate down
 * @param size the size of the heap
 */
template<class Key, class Other>
void percolateDown(set<Key, Other> *a, int hole, int size) {
    auto tmp = a[hole];
    size_t child = 0;
    while (hole * 2 <= size) {
        // !attention! it is 0-based here
        child = hole * 2 + 1;
        // left child
        if (child < size && a[child + 1].key < a[child].key) {
            // choose the right child
            ++child;
        }

        if (a[child].key < tmp.key) {
            a[hole] = a[child];
            hole = child;
        } else {
            break;
        }
    }
    a[hole] = tmp;
}

复杂度分析

To be done.

使用决策树分析：根节点代表原始序列$a_1a_2a_3\dots a_n$

则每一个叶子结点的序列都代表一个排序结果，也是一个排列！

关键证明：

$$\log(n!) = \Theta(n\log n)$$

Exchange Sort

交换排序的核心是逆序元素对的交换，例如如果我需要递增排序，那每一次交换操作可以表示为：

$$\exists x_1,x_2((x_1 < x_2 )\wedge( \text{index}(x_1) > \text{index}(x_2)) )$$

Bubble Sort

template<class Key, class Other>
void BubbleSort(set<Key, Other> *a, int size) {
    bool flag = true;
    for (int i = 1; i < size && !flag; i++) {
        flag = false;
        for (int j = 0; j < size - i; j++) {
            if (a[j + 1].key < a[j].key) {
                // swap!
                std::swap(a[j + 1], a[j]);
                flag = true;
            }
        }
    }
}

Quick Sort

快速排序和冒泡排序类似，也是一种非常经典的选择排序的算法。但是时间复杂度更低，并且快速排序被认为是一种最快的内排序算法。

快速排序在相邻的内存中作比较！

Intuition：设置基准元素pivot。

因此快速排序的伪代码如下：

选择界点。
左右区间根据界点进行划分。
处理左右半段：
- 找到第一个大于界点的节点（从左到右遍历）
- 找到第一个小于界点的节点（从右向左遍历）
- 交换这两个元素
直到完全划分成左右两个部分。

然后对子数组进行递归实现即可。

How to choose pivot?

使用待排序元素的第一个元素作为标准元素。
- 最坏时间复杂度是平方级的
随机化快排
使用采样法取出中值。

代码实现

我们首先实现首元素为标准元素的快速排序算法，核心函数在于partition（即在取定划分之后处理左右两侧的情况），同时为了更方便的实现递归函数（分治法），我们使用包裹函数的设计：

template<class Key, class Other>
int partition(set<Key, Other> *a, int low, int high) {
    set<Key, Other> pivot = a[low];
    int i = low + 1;
    int j = high;

    while (true) {
        while (i <= j && a[i].key <= pivot.key) {
            i++;
        }

        while (i <= j && a[j].key > pivot.key) {
            j--;
        }

        if (i >= j) {
            break;
        }
        std::swap(a[i], a[j]);
    }
    std::swap(a[low], a[j]);
    return j;
}

template<class Key, class Other>
void QuickSort(set<Key, Other> *a, int size) {
    Quicksort(a, 0, size - 1);
}

template<class Key, class Other>
void Quicksort(set<Key, Other> *a, int low, int high) {

    if (low >= high) {
        return;
        // the recursion end
    }
    // make the partition
    int mid = partition(a, low, high);

    // recursion
    Quicksort(a, low, mid - 1);
    Quicksort(a, mid + 1, high);
}

可以使用递推式证明在平均情况下，快速排序的时间复杂度为$O(N \log N)$

随机化快排

更换了一种选择pivot的算法，因为选择首元素对于逆序数据的时间复杂度可以达到$O(N^2)$，因为不会有任何的交换发生。

template<class Key, class Other>
int partition(set<Key, Other> *a, int low, int high) {
    set<Key, Other> pivot = a[low];
    int i = low + 1;
    int j = high;

    while (true) {
        while (i <= j && a[i].key <= pivot.key) {
            i++;
        }

        while (i <= j && a[j].key > pivot.key) {
            j--;
        }

        if (i >= j) {
            break;
        }

        std::swap(a[i], a[j]);
    }
    std::swap(a[low], a[j]);
    return j;
}

template<class Key, class Other>
int randomizedPartition(set<Key, Other> *a, int low, int high) {
    // Generate a random index between low and high
    int randomIndex = low + rand() % (high - low + 1);

    // Swap the randomly chosen pivot with the first element
    std::swap(a[low], a[randomIndex]);

    // Proceed with the normal partition logic
    set<Key, Other> pivot = a[low];
    int i = low + 1;
    int j = high;

    while (true) {
        while (i <= j && a[i].key <= pivot.key) {
            i++;
        }

        while (i <= j && a[j].key > pivot.key) {
            j--;
        }

        if (i >= j) {
            break;
        }

        std::swap(a[i], a[j]);
    }
    std::swap(a[low], a[j]);
    return j;
}

template<class Key, class Other>
void QuickSort(set<Key, Other> *a, int size) {
    Quicksort(a, 0, size - 1);
}

template<class Key, class Other>
void Quicksort(set<Key, Other> *a, int low, int high) {

    if (low >= high) {
        return;
        // the recursion end
    }
    // make the partition
    int mid = partition(a, low, high);

    // recursion
    Quicksort(a, low, mid - 1);
    Quicksort(a, mid + 1, high);
}

template<class Key, class Other>
void randomizedQuicksort(set<Key, Other> *a, int low, int high) {
    if (low >= high) {
        return;// The recursion ends
    }

    // Make the partition using randomizedPartition
    int mid = randomizedPartition(a, low, high);

    // Recursion
    randomizedQuicksort(a, low, mid - 1);
    randomizedQuicksort(a, mid + 1, high);
}

template<class Key, class Other>
void RandomizedQuickSort(set<Key, Other> *a, int size) {
    randomizedQuicksort(a, 0, size - 1);
}

Merge Sort

归并排序的思想非常简单，给定$A$，$B$两个有序的数组，现在需要合并这两个数组并保持其有序性。因为$A$,$B$的有序性，只需要线性扫描一遍就可以实现。在快速排序中，使用了尾递归的方式由大化小，而在归并排序中也是类似，拆分至小数组并把小数组merge到大数组。

/**
 * @brief merge the two sorted array, one is [left, mid -1], and the other is [mid, right]
 * 
 * @tparam Key 
 * @tparam Other 
 */
template<class Key, class Other>
void Merge(set<Key, Other> *a, int left, int mid, int right) {
    set<Key, Other>* tmp = new set<Key, Other>[right - left + 1];

    int i = left, j = mid, k = 0;

    while (i < mid && j <= right) {
        // the two sorted list doesn't end
        if (a[i].key < a[j].key) {
            tmp[k++] = a[i++];
        } else {
            tmp[k++] = a[j++];
        }
    }

    while (i < mid) {
        tmp[k++] = a[i++];
    }

    while (j <= right) {
        tmp[k++] = a[j++];
    }

    // move the sorted array to the original list
    for (i = 0, k = left; k <= right; i++, k++) {
        a[k] = tmp[i];
    }

    delete[] tmp;
}

template<class Key, class Other>
void MergeSort_(set<Key, Other> *a, int left, int right) {
    int mid = (left + right) / 2;
    if (left == right) {
        return;
    }

    MergeSort_(a, left, mid);
    MergeSort_(a, mid + 1, right);
    Merge(a, left, mid + 1, right);
}

template<class Key, class Other>
void MergeSort(set<Key, Other> *a, int size) {
    MergeSort_(a, 0, size - 1);
}

Bucket Sort

基数排序的思想非常简单，例如在排序非负十进制整数的时候，按照个位数的取值把不同的数放在不同的口袋中，收集之后再倒出。

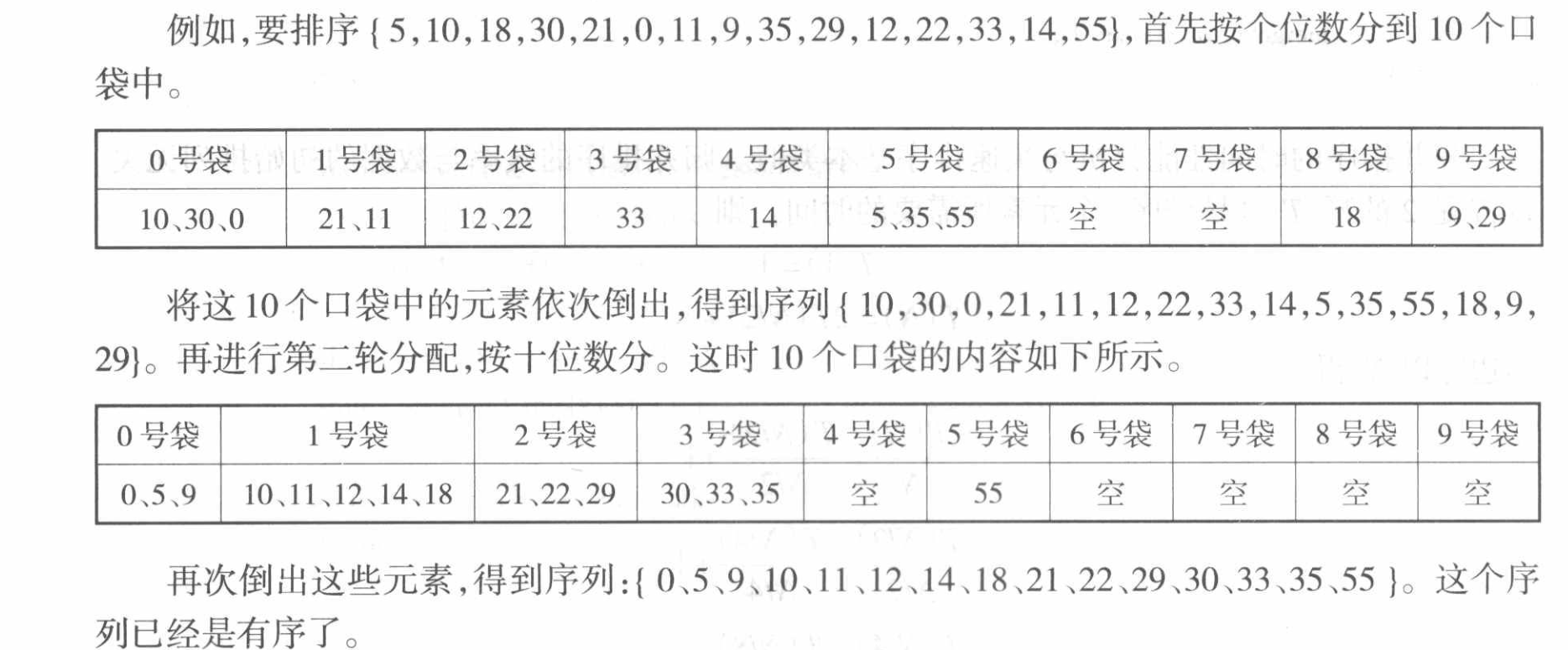
排序非负十进制整数

注意在上文的例子中，也可以先排十位数，只是需要注意在每个桶内的输入和输出的顺序要保持一致。

本质上和链表有点像！

template<class Other>
void BucketSort(node<Other> *&p) {
    node<Other> *bucket[10], *last[10], *tail;
    int max = 0, len = 0;

    // find the maximum key
    for (tail = p; tail != nullptr; tail = tail->next) {
        max = std::max(tail->data.key, max);
    }

    // find the length
    if (max == 0) {
        len = 0;
    } else {
        while (max > 0) {
            ++len;
            max /= 10;
        }
    }

    // starting the bucket sort
    int base = 1;
    for (int i = 1; i < len; i++, base *= 10) {
        // clear all the bucket
        for (int j = 0; j < 9; j++) {
            bucket[j] = last[j] = nullptr;
        }

        // allocate bucket for every element
        while (p != nullptr) {
            int k = ((p->data.key) / base) % 10;

            // add to different bucket!
            if (bucket[k] == nullptr) {
                // remains empty
                bucket[k] = last[k] = p;
            } else {
                last[k]->next = p;
                last[k] = last[k]->next;
            }
            p = p->next;
        }

        p = nullptr;
        // reconstruct, now p is the beginning and tail is the tail
        for (int j = 0; j < 9; j++) {
            if (bucket[j] == nullptr) {
                continue;
            }

            if (p == nullptr) {
                p = bucket[j];
            } else {
                tail->next = bucket[j];
            }

            tail = last[j];
        }

        tail->next = nullptr;
    }
}

Sort in STL

在STL中已经实现了sort和stable_sort，使用非常的简单。

`less` and `greater`

在 C++ 标准模板库（STL）中，less 和 greater 是两个功能强大的比较函数对象（functor），它们主要用于排序和比较操作。以下是对这两个函数对象的详细介绍：

`std::less`

定义：std::less 是一个函数对象，用于判断左侧的值是否小于右侧的值。
用法：它可以用于 STL 中的容器（如 std::set、std::map）以及排序算法（如 std::sort）。

示例：

#include <iostream>
#include <vector>
#include <algorithm>

int main() {
    std::vector<int> vec = {4, 2, 3, 1};

    // 使用 std::less 进行排序
    std::sort(vec.begin(), vec.end(), std::less<int>());

    for (int num : vec) {
        std::cout << num << " "; // 输出：1 2 3 4
    }
    return 0;
}

`std::greater`

定义：std::greater 是一个函数对象，用于判断左侧的值是否大于右侧的值。
用法：与 std::less 类似，它也可以用于 STL 容器和排序操作，通常用于实现降序排序。

示例：

#include <iostream>
#include <vector>
#include <algorithm>

int main() {
    std::vector<int> vec = {4, 2, 3, 1};

    // 使用 std::greater 进行降序排序
    std::sort(vec.begin(), vec.end(), std::greater<int>());

    for (int num : vec) {
        std::cout << num << " "; // 输出：4 3 2 1
    }
    return 0;
}

All Codes

所有的排序算法的代码：

// For all kinds of sorting algorithms
#include <cstdlib>
#include <iostream>
#include <queue>
#include <random>

template<class KEY, class OTHER>
struct set {
    KEY key = KEY();
    OTHER other = OTHER();
};

// Define SortFunction as a function pointer type
template<class Key, class Other>
using SortFunction = void (*)(set<Key, Other> *, int);

// Simple insertion sort
template<class Key, class Other>
void simpleInsertSort(set<Key, Other> *a, int size) {
    int k;
    set<Key, Other> tmp;

    // Start sorting
    for (int i = 1; i < size; i++) {
        tmp = a[i];
        for (k = i - 1; k >= 0 && tmp.key < a[k].key; --k) {
            a[k + 1] = a[k];
        }
        a[k + 1] = tmp;
    }
}

template<class Key, class Other>
void shellSort(set<Key, Other> *a, int size) {
    int step, i, j;
    set<Key, Other> tmp;

    for (step = size / 2; step > 0; step /= 2) {
        // shell array, finally is 1
        // do insert sort with stepsize of step
        for (i = step; i < size; i++) {
            tmp = a[i];
            for (j = i - step; j >= 0 && a[j].key > tmp.key; j -= step) {
                a[j + step] = a[j];
            }
            a[j + step] = tmp;
        }
    }
}

template<class Key, class Other>
void heapSort(set<Key, Other> *a, int size) {
    // Use a custom comparator for a min-heap
    auto cmp = [](const set<Key, Other> &lhs, const set<Key, Other> &rhs) {
        return lhs.key > rhs.key;// Min-heap: smaller key has higher priority
    };

    std::priority_queue<set<Key, Other>, std::vector<set<Key, Other>>, decltype(cmp)> pq(cmp);

    // Build the heap
    for (int i = 0; i < size; i++) {
        pq.push(a[i]);
    }

    // Extract elements from the heap in sorted order
    for (int i = 0; i < size; i++) {
        a[i] = pq.top();
        pq.pop();
    }
}

template<class Key, class Other>
void OwnHeapSort(set<Key, Other> *a, int size) {
    for (int i = size / 2 - 1; i >= 0; i--) {
        // build for all nodes
        percolateDown(a, i, size);
    }

    // dequeue
    /*
    i is the size of the current heap
    std::swap(a[0], a[i]) means pop the first element of the heap (swap with the ith element at the back)
    then use percolatedown to make the heap sorted again.(Use for a[0] only)
    */
    for (int i = size - 1; i > 0; i--) {
        std::swap(a[0], a[i]);
        percolateDown(a, 0, i);
    }
}

/**
 * @brief percolate down for the heap sort
 * 
 * @tparam Key 
 * @tparam Other 
 * @param a the array to be sorted
 * @param hole the starting position of percolate down
 * @param size the size of the heap
 */
template<class Key, class Other>
void percolateDown(set<Key, Other> *a, int hole, int size) {
    auto tmp = a[hole];
    int child = 0;
    while (hole * 2 + 1 < size) {
        // !attention! it is 0-based here
        child = hole * 2 + 1;
        // left child
        if (child != size - 1 && a[child + 1].key > a[child].key) {
            // choose the right child
            ++child;
        }

        if (a[child].key > tmp.key) {
            a[hole] = a[child];
            hole = child;
        } else {
            break;
        }
    }
    a[hole] = tmp;
}

template<class Key, class Other>
int partition(set<Key, Other> *a, int low, int high) {
    set<Key, Other> pivot = a[low];
    int i = low + 1;
    int j = high;

    while (true) {
        while (i <= j && a[i].key <= pivot.key) {
            i++;
        }

        while (i <= j && a[j].key > pivot.key) {
            j--;
        }

        if (i >= j) {
            break;
        }

        std::swap(a[i], a[j]);
    }
    std::swap(a[low], a[j]);
    return j;
}

template<class Key, class Other>
int randomizedPartition(set<Key, Other> *a, int low, int high) {
    // Generate a random index between low and high
    int randomIndex = low + rand() % (high - low + 1);

    // Swap the randomly chosen pivot with the first element
    std::swap(a[low], a[randomIndex]);

    // Proceed with the normal partition logic
    set<Key, Other> pivot = a[low];
    int i = low + 1;
    int j = high;

    while (true) {
        while (i <= j && a[i].key <= pivot.key) {
            i++;
        }

        while (i <= j && a[j].key > pivot.key) {
            j--;
        }

        if (i >= j) {
            break;
        }

        std::swap(a[i], a[j]);
    }
    std::swap(a[low], a[j]);
    return j;
}

template<class Key, class Other>
void QuickSort(set<Key, Other> *a, int size) {
    Quicksort(a, 0, size - 1);
}

template<class Key, class Other>
void Quicksort(set<Key, Other> *a, int low, int high) {

    if (low >= high) {
        return;
        // the recursion end
    }
    // make the partition
    int mid = partition(a, low, high);

    // recursion
    Quicksort(a, low, mid - 1);
    Quicksort(a, mid + 1, high);
}

template<class Key, class Other>
void randomizedQuicksort(set<Key, Other> *a, int low, int high) {
    if (low >= high) {
        return;// The recursion ends
    }

    // Make the partition using randomizedPartition
    int mid = randomizedPartition(a, low, high);

    // Recursion
    randomizedQuicksort(a, low, mid - 1);
    randomizedQuicksort(a, mid + 1, high);
}

template<class Key, class Other>
void RandomizedQuickSort(set<Key, Other> *a, int size) {
    randomizedQuicksort(a, 0, size - 1);
}

template<class Key, class Other>
void BubbleSort(set<Key, Other> *a, int size) {
    bool flag = true;
    for (int i = 1; i < size && flag; i++) {
        flag = false;
        for (int j = 0; j < size - i; j++) {
            if (a[j + 1].key < a[j].key) {
                // swap!
                std::swap(a[j + 1], a[j]);
                flag = true;
            }
        }
    }
}

template<class Key, class Other>
void selectSort(set<Key, Other> *a, int size) {
    for (int i = 0; i < size - 1; i++) {
        int min = i;
        for (int j = i + 1; j < size; j++) {
            // the unsorted array
            if (a[j].key < a[min].key) {
                // find the minimum element
                min = j;
            }
        }
        std::swap(a[i], a[min]);
    }
}

/**
 * @brief merge the two sorted array, one is [left, mid -1], and the other is [mid, right]
 * 
 * @tparam Key 
 * @tparam Other 
 */
template<class Key, class Other>
void Merge(set<Key, Other> *a, int left, int mid, int right) {
    set<Key, Other> *tmp = new set<Key, Other>[right - left + 1];

    int i = left, j = mid, k = 0;

    while (i < mid && j <= right) {
        // the two sorted list doesn't end
        if (a[i].key < a[j].key) {
            tmp[k++] = a[i++];
        } else {
            tmp[k++] = a[j++];
        }
    }

    while (i < mid) {
        tmp[k++] = a[i++];
    }

    while (j <= right) {
        tmp[k++] = a[j++];
    }

    // move the sorted array to the original list
    for (i = 0, k = left; k <= right; i++, k++) {
        a[k] = tmp[i];
    }

    delete[] tmp;
}

template<class Key, class Other>
void MergeSort_(set<Key, Other> *a, int left, int right) {
    int mid = (left + right) / 2;
    if (left == right) {
        return;
    }

    MergeSort_(a, left, mid);
    MergeSort_(a, mid + 1, right);
    Merge(a, left, mid + 1, right);
}

template<class Key, class Other>
void MergeSort(set<Key, Other> *a, int size) {
    MergeSort_(a, 0, size - 1);
}

//implementation of bucket sort
template<class Other>
struct node {
    set<int, Other> data;
    node *next;

    node() {
        next = nullptr;
    }

    node(const set<int, Other> &d) {
        data = d;
        next = nullptr;
    }
};

template<class Other>
void BucketSort(node<Other> *&p) {
    node<Other> *bucket[10], *last[10], *tail;
    int max = 0, len = 0;

    // find the maximum key
    for (tail = p; tail != nullptr; tail = tail->next) {
        max = std::max(tail->data.key, max);
    }

    // find the length
    if (max == 0) {
        len = 0;
    } else {
        while (max > 0) {
            ++len;
            max /= 10;
        }
    }

    // starting the bucket sort
    int base = 1;
    for (int i = 1; i < len; i++, base *= 10) {
        // clear all the bucket
        for (int j = 0; j < 9; j++) {
            bucket[j] = last[j] = nullptr;
        }

        // allocate bucket for every element
        while (p != nullptr) {
            int k = ((p->data.key) / base) % 10;

            // add to different bucket!
            if (bucket[k] == nullptr) {
                // remains empty
                bucket[k] = last[k] = p;
            } else {
                last[k]->next = p;
                last[k] = last[k]->next;
            }
            p = p->next;
        }

        p = nullptr;
        // reconstruct, now p is the beginning and tail is the tail
        for (int j = 0; j < 9; j++) {
            if (bucket[j] == nullptr) {
                continue;
            }

            if (p == nullptr) {
                p = bucket[j];
            } else {
                tail->next = bucket[j];
            }

            tail = last[j];
        }

        tail->next = nullptr;
    }
}

int generate_random() {
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_int_distribution<> dis(1, 100000);
    return dis(gen);
}

// Helper function to generate a random string of given length
std::string generate_random_string(int length) {
    const char charset[] = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ";
    const int charset_size = sizeof(charset) - 1;

    std::string result;
    result.reserve(length);

    for (int i = 0; i < length; i++) {
        result += charset[rand() % charset_size];
    }

    return result;
}

// Test function that accepts a function pointer
template<class Key, class Other>
bool test_sort(SortFunction<Key, Other> sortFunc) {
    // Generate a random array of size 1000
    const int size = 1000;
    set<Key, Other> arr[size];

    // Fill the array with random data
    for (int i = 0; i < size; i++) {
        arr[i].key = generate_random();           // Random integer key
        arr[i].other = generate_random_string(10);// Random string of length 10
    }

    // Sort the array using the provided sorting function
    sortFunc(arr, size);

    // Check if the array is sorted in ascending order
    for (int i = 1; i < size; i++) {
        if (arr[i].key < arr[i - 1].key) {
            return false;// Array is not sorted
        }
    }

    return true;// Array is sorted
}


int main() {
    SortFunction<int, std::string> sortFunc[] = {
            simpleInsertSort,
            shellSort,
            heapSort,
            OwnHeapSort,
            QuickSort,
            RandomizedQuickSort,
            BubbleSort,
            selectSort,
            MergeSort,
    };

    std::vector<std::string> name = {
            "simpleInsertSort",
            "shellSort",
            "heapSort",
            "OwnHeapSort",
            "QuickSort",
            "RandomizedQuickSort",
            "BubbleSort",
            "selectSort",
            "MergeSort",
    };

    for (int i = 0; i < 9; i++) {
        if (test_sort(sortFunc[i]) == true) {
            std::cout << name[i] << " pass successfully!" << std::endl;
        } else {
            std::cout << name[i] << " fail!" << std::endl;
        }
    }


    return 0;
}

Algorithm > SJTU CS0501(H) Data Structure

#Finished #C/C++ #Sorting Algorithms #Merge Sort #Quick Sort

Algorithm-Sorting

https://xiyuanyang-code.github.io/posts/Algorithm-Sorting/

Author

Xiyuan Yang

Posted on

March 29, 2025

Updated on

May 19, 2025

Licensed under

DataStructure-Fenwick-Tree Previous

DataStructure-Tree-Binary-Search-Tree-AVL-Tree Next

Algorithm-Sorting

Sorting Algorithms

Introduction

Insert Sort

直接插入排序

Code

复杂度分析

二分插入排序

希尔排序

Select Sort

Simple Select Sort

Heap Sort

可否优化？

复杂度分析

Exchange Sort

Bubble Sort

Quick Sort

How to choose pivot?

代码实现

随机化快排

Merge Sort

Bucket Sort

Sort in STL

less and greater

std::less

std::greater

All Codes

`less` and `greater`

`std::less`

`std::greater`