Algorithm-MCTS

Monte Carlo Tree Search

Introduction

今天介绍非常经典的AI领域的搜索算法之一：蒙特卡洛树搜索（Monte Carlo Tree Search）！

传统的树搜索算法

树搜索算法是非常常见的一类算法，例如在棋类游戏中，我们需要使用树搜索算法来找到下一步（近似）最优的策略来提高胜率。但是传统的树搜索算法在解决这个问题的时候存在如下的局限性：

  • 搜索空间问题

    • 传统的树搜索枚举算法 (O(bd)O(b^d))在面对较大的搜索空间时效率非常低。

  • 高分支因子问题 (Branching Factor)

    • Binary Tree: 2
    • Chess: 35
    • Go: 250

    这里的分支因子就是上文的 bb ，即每扩张一个节点需要扩展出多少个子节点。显然这个提升是指数级别的，面对复杂决策问题是计算机很难在有限的时间内找到可行的算法。

不过，一些优化算法已经对这个问题做出了大幅度的剪枝，例如 Alpha-Beta 剪枝 (O(bd2))(O(b^{\frac{d}{2}}))：但是无法有效解决高分支因子问题。类似的解决思路包括启发式算法的设计，但是启发式算法严格依赖专业知识和代价函数的设计，设计一个通用性的算法存在较大的难度。

有关Alpha-Beta剪枝算法和极大值极小值算法同样非常有趣！准备开坑。

问题出在哪？

显然，让计算机在众多的可能性中模拟出当前最优决策是一件非常困难的事情，因此，我们不妨把问题适当放宽，我们只是希望走出相对好的一步，而并不严格要求“最好”的一步呢？（在实际比赛中，你也不可能要求每一位旗手每一步都下出最优解）。

对于传统的暴力和剪枝算法，其最终目标都是求出严格全局最小值，因此带来极大的计算成本。或许，我们并不需要计算的那么仔细！Just Randomly！

蒙特卡洛算法

蒙特卡洛算法是基于随机数和概率的一种算法。

简单来说，就是与其进行复杂的确定性演算法，蒙特卡洛算法背靠强大的概率论，使其在较低的时空开销下就可以拟合出较高精度的结果。

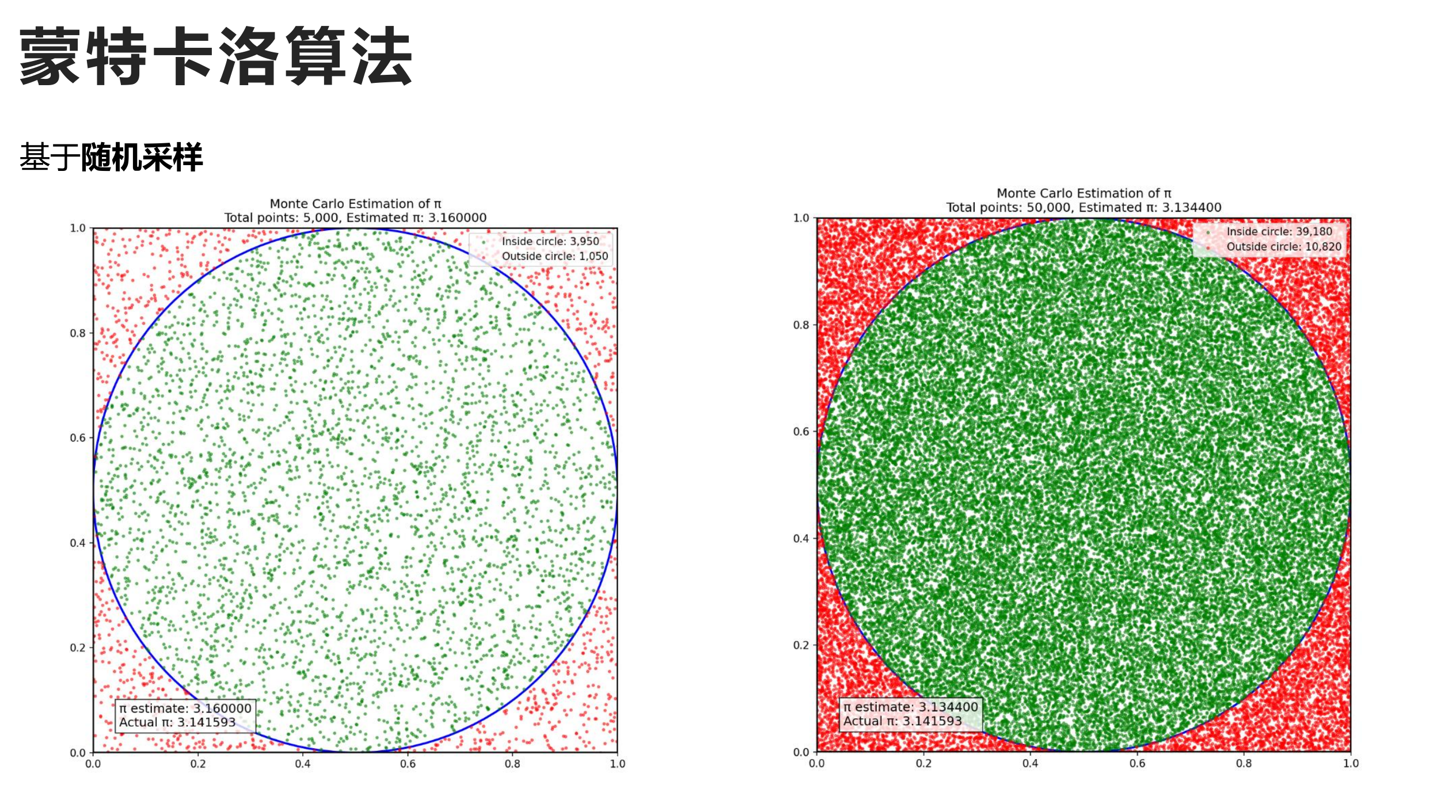
基于蒙特卡洛算法估算圆周率

因此，我们便可以实现基于蒙特卡洛算法的树搜索，简称蒙特卡洛树搜索。

Algorithms

Nodes

在蒙特卡洛树搜索中，我们需要在树的每一个节点中储存如下信息：

  • 状态信息： 节点对应的状态（当前棋局的对弈情况）
  • 动作信息：从父节点到当前节点需要采取的动作
  • 访问次数：这个节点在算法中是否被访问过？这对后续算=算法的计算非常关键。
  • 累计奖励：蒙特卡洛算法的核心，将决策量化的指标
  • 父节点指针和子节点列表
  • bool：是否完全扩展：即该节点是否完全扩展（其后续下一步可能的情况是否全部添加到树中）

Flowchart

MCTS

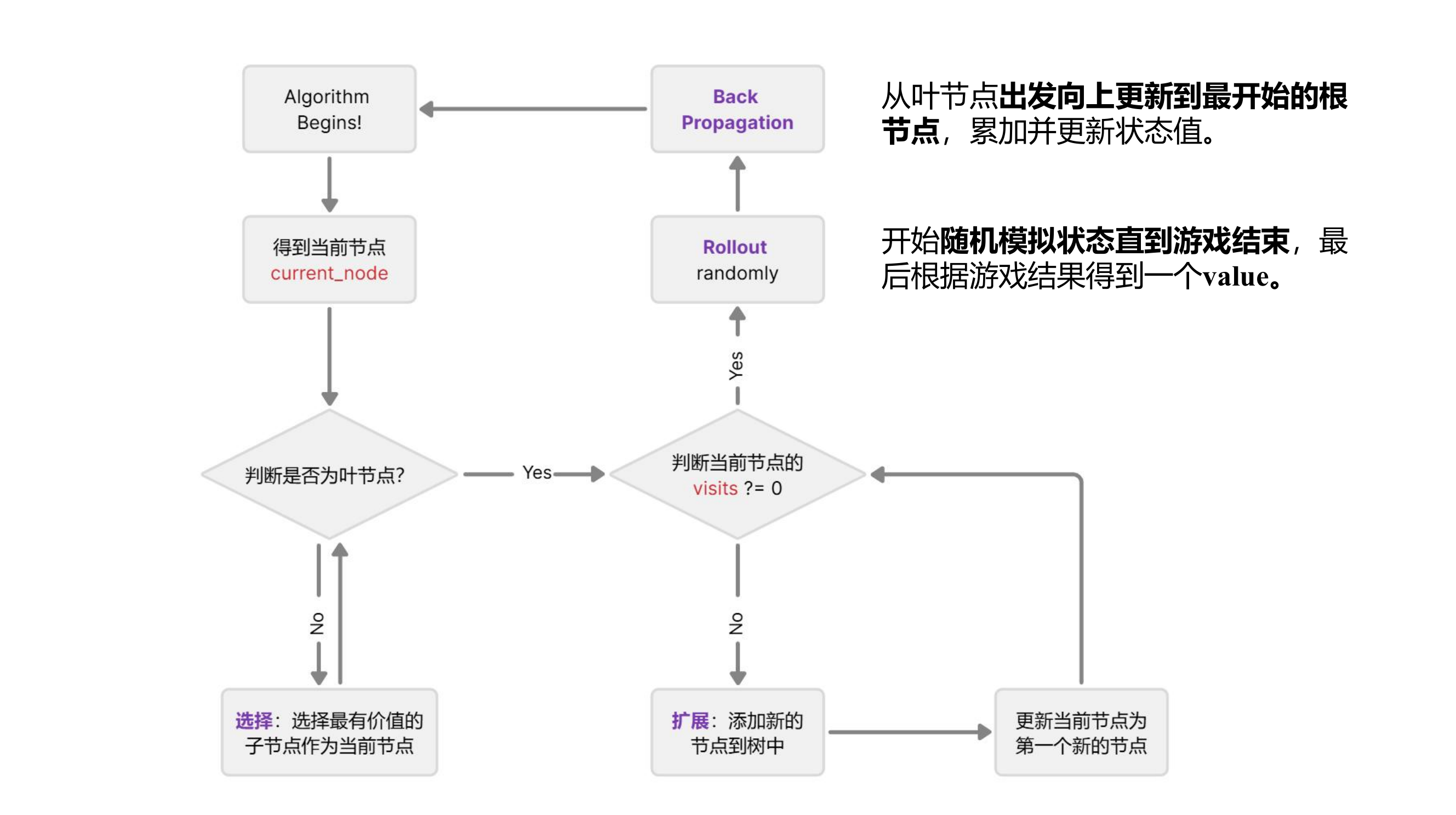
在每一次蒙特卡洛算法的时候，我们需要从当前状态qsq_s出发（ss代表目前游戏的轮数），通过算法计算找到“最优的下一步”，也就是说问题可以转化为：

给定当前状态 $ q_s $（表示第 $ s $ 轮的状态），我们需要找到下一个状态 $ q_{s+1} $，它对应的动作 $ a $ 应该满足以下条件：

a∗=arg⁡max⁡a∈A(qs)E[R(qs,a)]a^* = \arg\max_{a \in \mathcal{A}(q_s)} \mathbb{E}[R(q_s, a)]

E[R(qs,a)]\mathbb{E}[R(q_s, a)]代表在对应动作下所获得的期望，也就是选择最能让我赢得比赛的子节点。

因此，算法是从当前节点开始的，作为current_node，接下来，蒙特卡洛算法会向下探索尝试更新每一个子节点的value值。首先进入第一个while循环：沿着子节点向下走直到当前节点为叶节点，那如何选择沿着哪一个子节点向下走呢？在这里给出UCB1公式，算法将会选择UCB值最大的子节点进行探索。

UCB1

UCB1(v′)=Q(v′)N(v′)+c×ln⁡N(v)N(v′)\text{UCB1}(v') = \frac{Q(v')}{N(v')} + c \times \sqrt{\frac{\ln N(v)}{N(v')}}

  • v′v' 是子节点

  • Q(v′)Q(v') 是子节点的累计价值

  • N(v′)N(v') 是子节点的访问次数

  • N(v)N(v) 是父节点的访问次数

  • cc 是探索参数（通常设为2\sqrt{2}）

关于UCB有几条很有意思的性质：

  • UCB非常鼓励对未知节点的探索，显然当N(v′)N(v')为0是时，UCB的值会陷入无穷大，肯定会被选择。
  • UCB实现了对已知和未知的tradeoff，一方面，子节点访问次数少的节点会更有几率被选择到，另一方面，子节点访问次数多的节点的累计价值也会更高，如果其价值足够的高，确实能够为自己赢得再被探索一次的机会。

跳出第一个循环后，马上来到第二个循环，此时我们已经来到了叶节点，我们需要判断这个节点是否被探索过，如果没有被探索过，那此时就要进行rollout的模拟操作：从这个未被探索过的节点出发，随机模拟比赛的进行，直到比赛结束。如果被探索过了，那说明这个节点已经完成了rollout的模拟，此时需要进行叶节点的扩展操作，即添加新的节点到树中。

在rollout完成过后，会得到一个游戏结果，此时需要进行反向传播，即更新“来时路”上所有节点的value值，这里采用累加的方法。例如如果最终游戏结局的分数是20，那么路径上的所有节点的value都要加20。一直到回到最开始的节点，完成一次大迭代。

最终，蒙特卡洛算法会限制每一步的迭代次数，当迭代次数满了之后，就回到最开始的节点选择value最大的节点。因此，蒙特卡洛最关键的算法其实包含四个部分：选择(selection)，扩展（expansion），**模拟（rollout）**和 反向传播（Back Propagation）。

MCTS

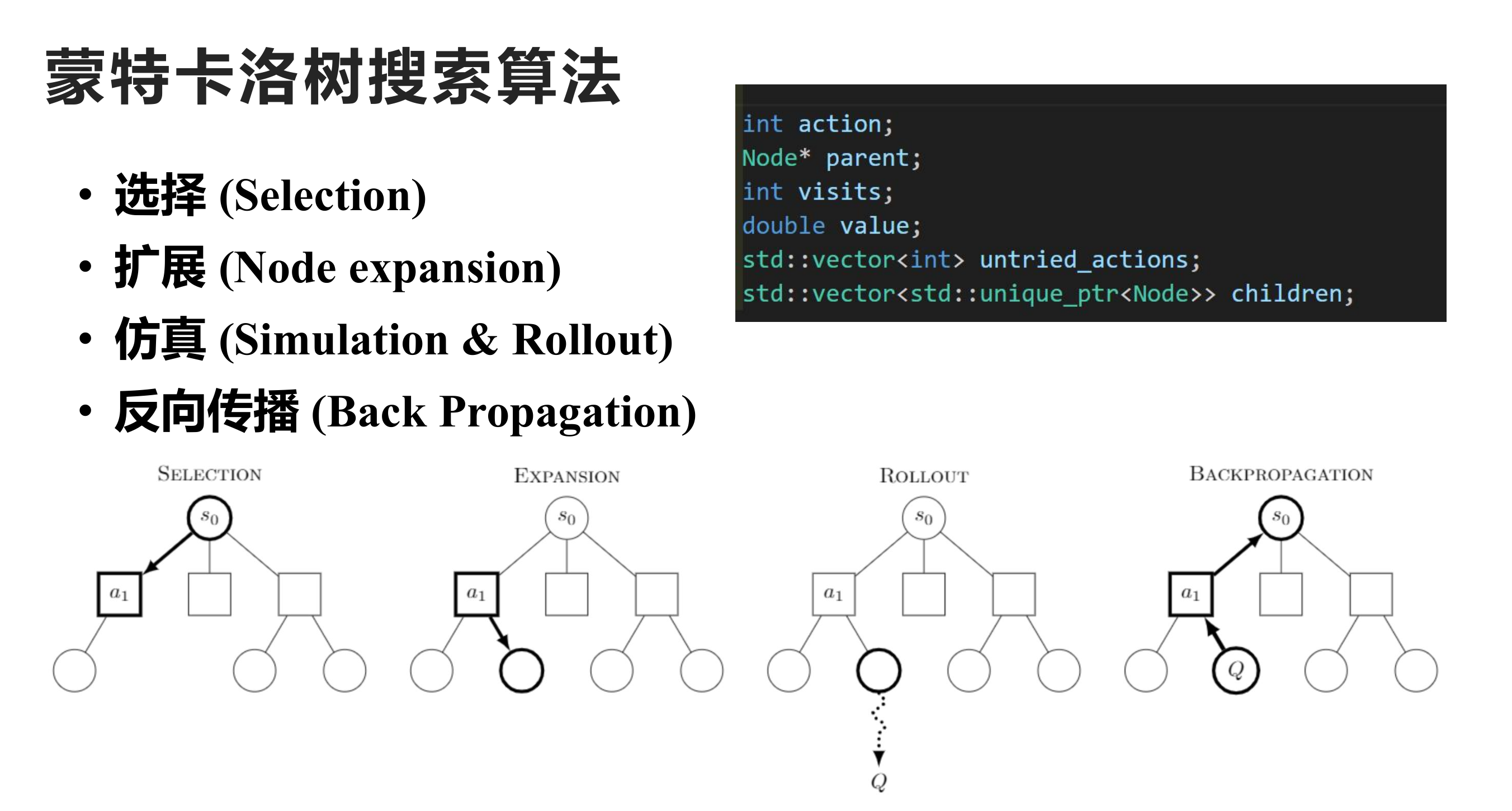
Implementation

Powered By GPT, to be done.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
import math
import random
from collections import defaultdict

class Node:
    def __init__(self, state, parent=None):
        self.state = state  # 游戏状态
        self.parent = parent  # 父节点
        self.children = []  # 子节点列表
        self.visits = 0  # 访问次数
        self.value = 0  # 节点价值
        self.untried_actions = self.state.get_legal_actions()  # 未尝试的动作

    def is_fully_expanded(self):
        return len(self.untried_actions) == 0
    
    def best_child(self, exploration_param=1.4):
        # 根据UCT公式选择最佳子节点
        return max(self.children, 
                   key=lambda child: child.value / (child.visits + 1e-6) + 
                   exploration_param * math.sqrt(2 * math.log(self.visits + 1) / (child.visits + 1e-6)))
    
    def expand(self):
        # 从未尝试的动作中选择一个动作进行扩展
        action = self.untried_actions.pop()
        next_state = self.state.perform_action(action)
        child_node = Node(next_state, parent=self)
        self.children.append(child_node)
        return child_node
    
    def is_terminal_node(self):
        return self.state.is_game_over()
    
    def rollout(self):
        # 模拟随机对局直到游戏结束
        current_state = self.state
        while not current_state.is_game_over():
            possible_actions = current_state.get_legal_actions()
            action = random.choice(possible_actions)
            current_state = current_state.perform_action(action)
        return current_state.game_result()
    
    def backpropagate(self, result):
        # 反向传播模拟结果
        self.visits += 1
        self.value += result
        if self.parent:
            self.parent.backpropagate(result)

class MCTS:
    def __init__(self, initial_state, iterations=1000):
        self.root = Node(initial_state)
        self.iterations = iterations
    
    def search(self):
        for _ in range(self.iterations):
            node = self._select()
            result = self._simulate(node)
            node.backpropagate(result)
        return self._best_action()
    
    def _select(self):
        # 选择阶段：从根节点开始，选择一个未完全扩展或非终止节点
        current_node = self.root
        while not current_node.is_terminal_node():
            if not current_node.is_fully_expanded():
                return current_node.expand()
            else:
                current_node = current_node.best_child()
        return current_node
    
    def _simulate(self, node):
        # 模拟阶段：从选定节点开始随机模拟
        if node.is_terminal_node():
            return node.state.game_result()
        return node.rollout()
    
    def _best_action(self):
        # 选择访问次数最多的子节点对应的动作
        if not self.root.children:
            return None
        return max(self.root.children, key=lambda child: child.visits).state.last_action

# 示例游戏状态类（需要根据具体游戏实现）
class GameState:
    def __init__(self):
        # 初始化游戏状态
        pass
    
    def get_legal_actions(self):
        # 返回当前状态下合法的动作列表
        return []
    
    def perform_action(self, action):
        # 执行动作并返回新的游戏状态
        new_state = GameState()
        # 更新状态...
        new_state.last_action = action
        return new_state
    
    def is_game_over(self):
        # 检查游戏是否结束
        return False
    
    def game_result(self):
        # 返回游戏结果（例如：1表示玩家1胜利，-1表示玩家2胜利，0表示平局）
        return 0

# 使用示例
if __name__ == "__main__":
    initial_state = GameState()
    mcts = MCTS(initial_state, iterations=1000)
    best_action = mcts.search()
    print(f"Best action: {best_action}")

Applications Nowadays

ICLR2025 AFlow

使用蒙特卡洛树搜索作为基本思想，使用Graph来存储一个Agentic Workflow，对于图的扩展，采用蒙特卡洛树搜索的模拟算法在极大的状态空间中尽可能搜索到优化后的结果，是一种自动化设计Agentic工作流的新颖思路。

Url: Aflow

Algorithm
#tutorial #MCTS
Algorithm-MCTS
https://xiyuanyang-code.github.io/posts/Algorithm-MCTS/
Author
Xiyuan Yang
Posted on
April 8, 2025
Updated on
July 10, 2025
Licensed under