Algorithm-Introduction

Algorithm_tutorial_section1

【写在前面的话】

本文是笔者自己算法课程的学习笔记，目前的学习内容主要是算法和数据结构基础（提前自学，笔者会在大一下学期系统学习），学习途径和资源主要是 Hello 算法（一本非常易入门的算法书！非常推荐！）。因此，此文章是Algorithm_tutorial的第一篇博客~，且大部分内容来自Hello算法原书，原创部分属于少数，笔者在此处只是按照自己的知识体系进行归纳总结并且尝试记录下来。希望大家都能愉快地开启自己的算法学习之旅~

Algorithm.Section1 Introduction

Introduction：

迭代与递归
时间复杂度
空间复杂度
数据结构的物理结构

一、算法复杂度分析

由于实际测试具有较大的局限性，因此我们可以考虑仅通过一些计算来评估算法的效率。这种估算方法被称为渐近复杂度分析（asymptotic complexity analysis），简称复杂度分析。

复杂度分析能够体现算法运行所需的时间和空间资源与输入数据大小之间的关系。它描述了随着输入数据大小的增加，算法执行所需时间和空间的增长趋势。这个定义有些拗口，我们可以将其分为三个重点来理解。

“时间和空间资源”分别对应时间复杂度（time complexity）和空间复杂度（space complexity）。
“随着输入数据大小的增加”意味着复杂度反映了算法运行效率与输入数据体量之间的关系。
“时间和空间的增长趋势”表示复杂度分析关注的不是运行时间或占用空间的具体值，而是时间或空间增长的“快慢”。（一种趋势！）

@迭代与递归

迭代：自下而上，小问题积累成大问题

递归：自上而下，大问题拆解成小问题

程序实现重复代码块执行的两种方式：

迭代（for循环，while循环）
递归

递归（recursion）是一种算法策略，通过函数调用自身来解决问题。它主要包含两个阶段。

递：程序不断深入地调用自身，通常传入更小或更简化的参数，直到达到“终止条件”。
归：触发“终止条件”后，程序从最深层的递归函数开始逐层返回，汇聚每一层的结果。

而从实现的角度看，递归代码主要包含三个要素。

终止条件：用于决定什么时候由“递”转“归”。
递归调用：对应“递”，函数调用自身，通常输入更小或更简化的参数。
返回结果：对应“归”，将当前递归层级的结果返回至上一层。

有关递归的时间问题和空间问题

递归函数每次调用自身时，系统都会为新开启的函数分配内存，以存储局部变量、调用地址和其他信息等。这将导致两方面的结果。

函数的上下文数据都存储在称为“栈帧空间”的内存区域中，直至函数返回后才会被释放。因此，递归通常比迭代更加耗费内存空间。（需要控制递归深度，否则过深的递归会导致栈的溢出错误）
有关栈帧空间：
栈帧空间是指在程序执行过程中，为每个函数调用分配的一块内存区域，用于存储该函数的局部变量、参数、返回地址以及其他控制信息。每次函数被调用时，都会在调用栈上创建一个新的栈帧，这个栈帧的生命周期与函数的执行周期相同。
1. 返回地址：当函数调用完成后，程序需要知道从哪里继续执行，因此返回地址会被压入栈帧中。
2. 参数：函数调用时传递给被调用函数的参数也会存储在栈帧中。
3. 局部变量：函数内部定义的局部变量会占用栈帧空间。
4. 控制信息：包括指向上一个栈帧的指针（帧指针），用于维护调用链。
栈帧的工作机制
- 入栈：当一个函数被调用时，首先将参数和返回地址压入栈中，然后分配空间给局部变量，形成新的栈帧。
- 出栈：当函数执行完毕时，局部变量和参数的空间被释放，返回地址被弹出，程序控制流转回调用该函数的位置。
栈帧的优点
- 自动管理：栈帧由系统自动管理，无需手动分配和释放内存。
- 高效性：由于栈的后进先出特性，内存分配和释放速度非常快。
递归调用函数会产生额外的开销。因此递归通常比循环的时间效率更低。
使用尾递归可以优化递归的效率（系统无需保存函数上一级的上下文）

有关递归树

我们在函数内递归调用了两个函数，这意味着从一个调用产生了两个调用分支。如图 2-6 所示，这样不断递归调用下去，最终将产生一棵层数为 n 的递归树（recursion tree）。

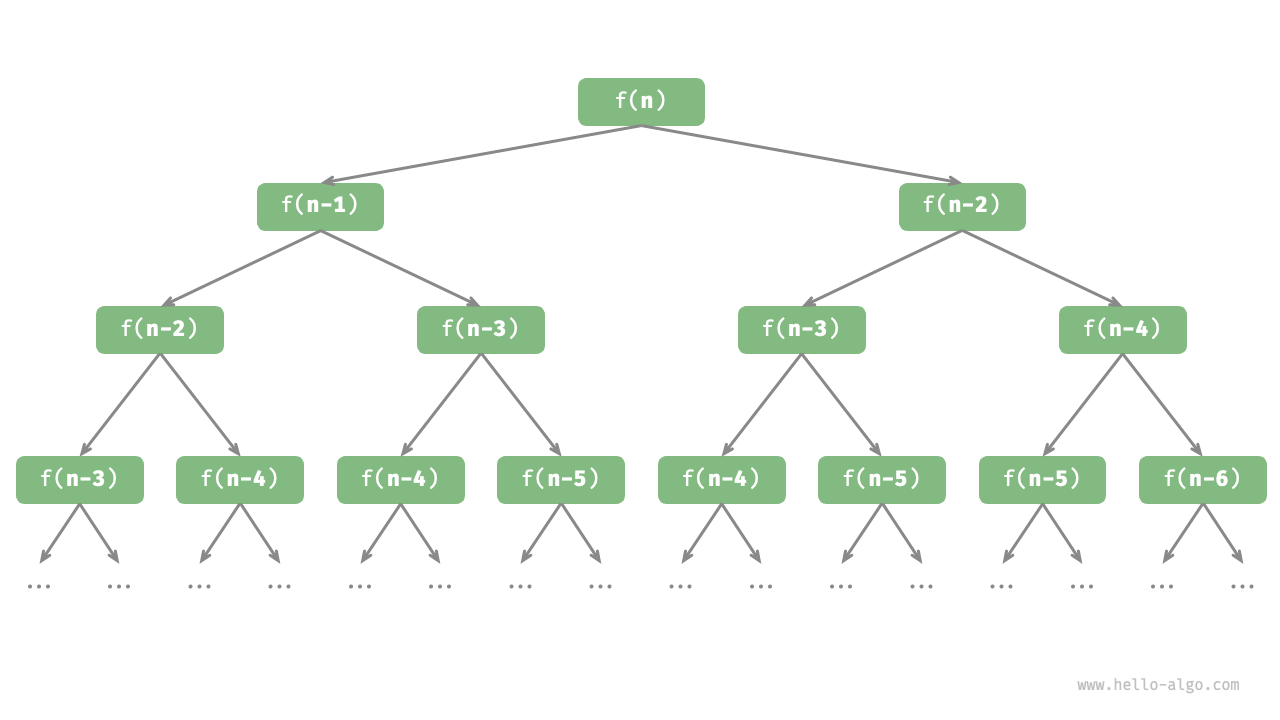
斐波那契数列的递归树

这种递归树可以达到指数阶的时间复杂度。

一定要理解递归的核心思想：分治！

从本质上看，递归体现了“将问题分解为更小子问题”的思维范式，这种分治策略至关重要。

从算法角度看，搜索、排序、回溯、分治、动态规划等许多重要算法策略直接或间接地应用了这种思维方式。
从数据结构角度看，递归天然适合处理链表、树和图的相关问题，因为它们非常适合用分治思想进行分析。

迭代和递归的本质与内在联系

以上述递归函数为例，求和操作在递归的“归”阶段进行。这意味着最初被调用的函数实际上是最后完成其求和操作的，这种工作机制与栈的“先入后出”原则异曲同工。

事实上，“调用栈”和“栈帧空间”这类递归术语已经暗示了递归与栈之间的密切关系。

递：当函数被调用时，系统会在“调用栈”上为该函数分配新的栈帧，用于存储函数的局部变量、参数、返回地址等数据。
归：当函数完成执行并返回时，对应的栈帧会被从“调用栈”上移除，恢复之前函数的执行环境。

def for_loop_recur(n: int) -> int:
    """使用迭代模拟递归"""
    # 使用一个显式的栈来模拟系统调用栈
    stack = []
    res = 0
    # 递：递归调用
    for i in range(n, 0, -1):
        # 通过“入栈操作”模拟“递”
        stack.append(i)
    # 归：返回结果
    while stack:
        # 通过“出栈操作”模拟“归”
        res += stack.pop()
    # res = 1+2+3+...+n
    return res

@时间复杂度

常数时间复杂度
线性时间复杂度
平方时间复杂度
指数阶时间复杂度
- 递归树的一分为二
对数阶时间复杂度
- 每轮缩减到一半
- 也会出现在递归树中（经典例题：快速幂计算）
线性对数阶时间复杂度（O(nlogn)）

def linear_log_recur(n: int) -> int:
    """线性对数阶"""
    if n <= 1:
        return 1
    # 一分为二，子问题的规模减小一半
    count = linear_log_recur(n // 2) + linear_log_recur(n // 2)
    # 与C++不同，//表示地板出发（整数截断）
    # 当前子问题包含 n 个操作
    for _ in range(n):
        count += 1
    # 代表当前需要执行的n次操作
    return count

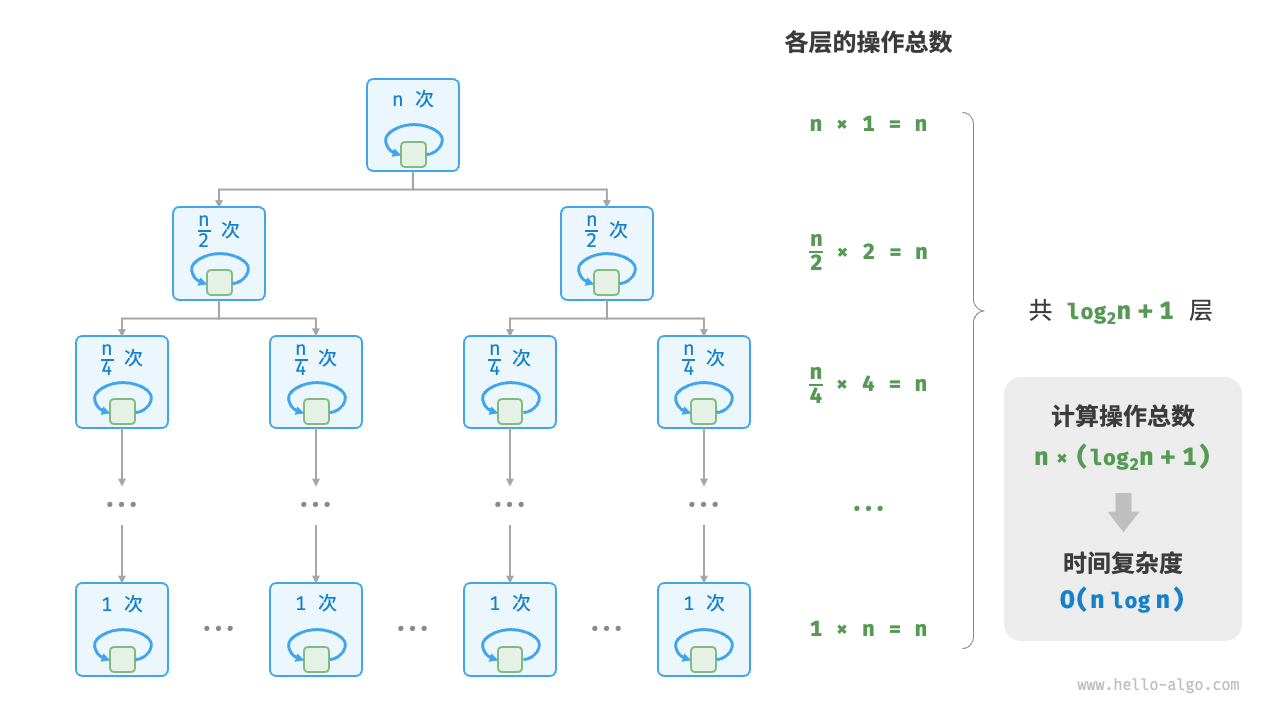
线性对数阶的时间复杂度

阶乘阶时间复杂度

def factorial_recur(n: int) -> int:
    """阶乘阶（递归实现）"""
    if n == 0:
        return 1
    count = 0
    # 从 1 个分裂出 n 个
    for _ in range(n):
        count += factorial_recur(n - 1)
    return count

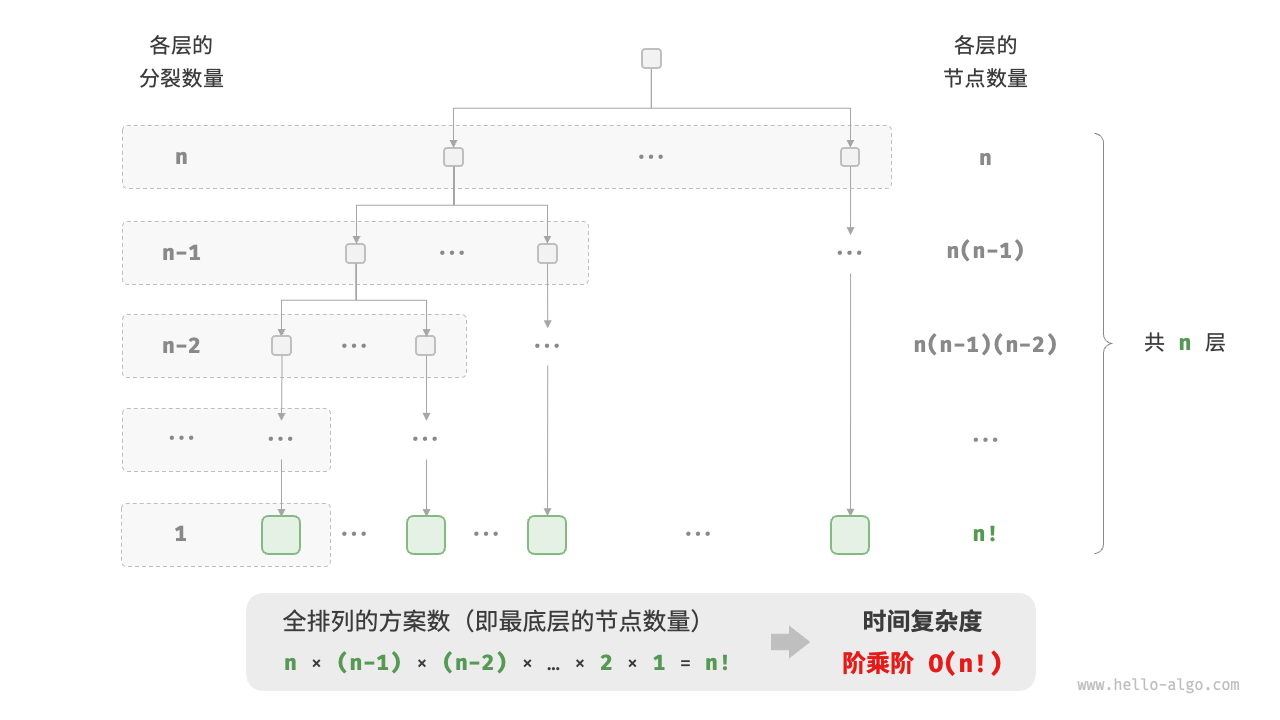
阶乘阶的时间复杂度

时间复杂度的分类：

最差时间复杂度
最佳时间复杂度

以上两个时间复杂度均与数据的分布存在联系，具有偶然性

平均时间复杂度

符号表示：

时间复杂度的符号表示法主要有三种：O、Ω 和 Θ，它们分别表示算法在不同情况下的性能表现。

大 O 表示法 (O(f(n)))：
- 描述：表示算法在最坏情况下的时间复杂度。
- 用途：用于描述算法的上界，即算法的执行时间不会超过某个函数的增长速度。
- 示例：如果一个算法的时间复杂度是 (O(n^2))，意味着在最坏情况下，算法的执行时间最多是输入规模的平方。
大 Ω 表示法 (Ω(f(n)))：
- 描述：表示算法在最好情况下的时间复杂度。
- 用途：用于描述算法的下界，即算法的执行时间至少是某个函数的增长速度。
- 示例：如果一个算法的时间复杂度是 (Ω(n))，意味着在最好情况下，算法的执行时间至少是输入规模的线性增长。
大 Θ 表示法 (Θ(f(n)))：
- 描述：表示算法在平均情况下的时间复杂度。
- 用途：用于描述算法的确界，即算法的执行时间既不会超过某个函数的上界，也不会低于某个函数的下界。
- 示例：如果一个算法的时间复杂度是 (Θ(n \log n))，意味着在所有情况下，算法的执行时间大致是输入规模的 (n \log n) 级别。

@空间复杂度

算法在运行过程中使用的内存空间主要包括以下几种。

输入空间：用于存储算法的输入数据。
暂存空间：用于存储算法在运行过程中的变量、对象、函数上下文等数据。
输出空间：用于存储算法的输出数据。

一般情况下，空间复杂度的统计范围是“暂存空间”加上“输出空间”。

暂存空间可以进一步划分为三个部分。

暂存数据：用于保存算法运行过程中的各种常量、变量、对象等。
栈帧空间：用于保存调用函数的上下文数据。系统在每次调用函数时都会在栈顶部创建一个栈帧，函数返回后，栈帧空间会被释放。
指令空间：用于保存编译后的程序指令，在实际统计中通常忽略不计。

在分析一段程序的空间复杂度时，我们通常统计暂存数据、栈帧空间和输出数据三部分。

class Node:
    """类"""
    def __init__(self, x: int):
        self.val: int = x              # 节点值
        self.next: Node | None = None  # 指向下一节点的引用

def function() -> int:
    """函数"""
    # 执行某些操作...
    return 0

def algorithm(n) -> int:  # 输入数据
    A = 0                 # 暂存数据（常量，一般用大写字母表示）
    b = 0                 # 暂存数据（变量）
    node = Node(0)        # 暂存数据（对象）
    c = function()        # 栈帧空间（调用函数）
    return A + b + c      # 输出数据

而与时间复杂度不同的是，我们通常只关注最差空间复杂度。这是因为内存空间是一项硬性要求，我们必须确保在所有输入数据下都有足够的内存空间预留。

以最差输入数据为准
以算法运行的峰值内存（注意不是累积量）为准

一些常见的空间复杂度：

常数阶空间复杂度
- 在循环中初始化变量或调用函数而占用的内存，在进入下一循环后就会被释放，因此不会累积占用空间，空间复杂度还是O(1)。

线性阶空间复杂度

def linear(n: int):
    """线性阶"""
    # 长度为 n 的列表占用 O(n) 空间
    nums = [0] * n
    # 长度为 n 的哈希表占用 O(n) 空间
    hmap = dict[int, str]()
    for i in range(n):
        hmap[i] = str(i)

def linear_recur(n: int):
    """线性阶（递归实现）"""
    print("递归 n =", n)
    if n == 1:
        return
    linear_recur(n - 1)
    # 在达到最深的递归深度的时候，会有n个变量n（涉及到局部变量）

平方阶空间复杂度

def quadratic(n: int):
    """平方阶"""
    # 二维列表占用 O(n^2) 空间
    num_matrix = [[0] * n for _ in range(n)]

num_matrix：这是一个变量名，用于存储生成的二维矩阵。

[[0] * n for _ in range(n)]：这是一个列表生成式，用于创建一个包含 n 个子列表的列表，每个子列表包含 n 个元素。

[0] * n：这一部分创建一个包含 n 个 0 的列表。例如，如果 n 是 3，则生成 [0, 0, 0]。
for _ in range(n)：这一部分用于重复创建上述的子列表 n 次。_ 是一个惯用的变量名，表示循环变量在循环体内未被使用。

def quadratic_recur(n: int) -> int:
    """平方阶（递归实现）"""
    if n <= 0:
        return 0
    # 数组 nums 长度为 n, n-1, ..., 2, 1
    nums = [0] * n
    return quadratic_recur(n - 1)

指数阶空间复杂度（二叉树）

def build_tree(n: int) -> TreeNode | None:
    """指数阶（建立满二叉树）"""
    if n == 0:
        return None
    root = TreeNode(0)
    root.left = build_tree(n - 1)
    root.right = build_tree(n - 1)
    return root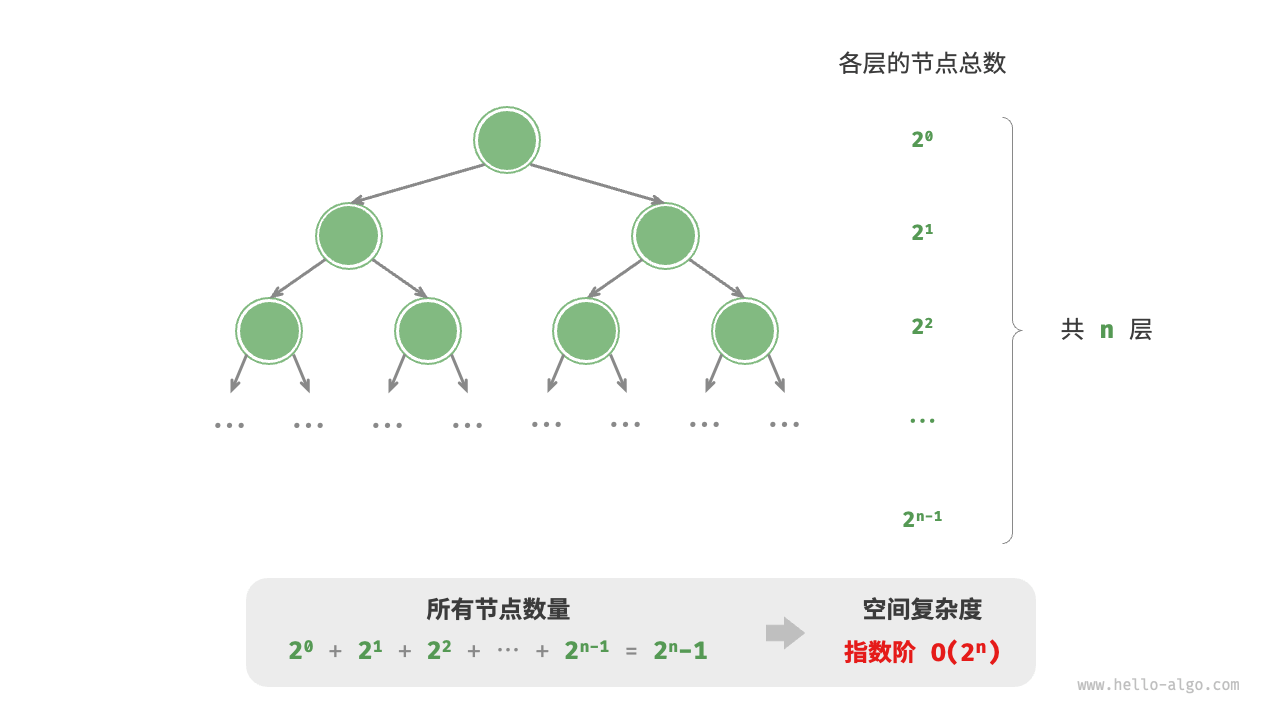

满二叉树产生的指数阶空间复杂度

对数阶空间复杂度

对数阶空间复杂度（(O(\log n))）在算法中并不如其他复杂度（如常数、线性、平方等）常见，因为对数阶通常与递归深度相关联。以下是一些可能具有对数阶空间复杂度的常见算法和场景：

递归算法：

二分查找：在递归实现中，二分查找的空间复杂度是 (O(\log n))，因为递归调用栈的深度是对数级别的。
快速排序：在最优情况下（即每次分区都能将数组均匀分割），快速排序的递归深度是 (O(\log n))，因此空间复杂度也是 (O(\log n))。
归并排序：尽管归并排序的时间复杂度是 (O(n \log n))，其递归实现的空间复杂度可以是 (O(\log n))（不包括用于存储结果的额外数组）。

快速排序（Quick Sort）

快速排序是一种分而治之的排序算法。它的基本思想是选择一个基准元素（pivot），然后将数组分成两个子数组，一个包含所有小于基准元素的元素，另一个包含所有大于基准元素的元素，然后递归地对这两个子数组进行排序。

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    else:
        pivot = arr[len(arr) // 2]
        left = [x for x in arr if x < pivot]
        middle = [x for x in arr if x == pivot]
        right = [x for x in arr if x > pivot]
        return quick_sort(left) + middle + quick_sort(right)

# 示例使用
arr = [3, 6, 8, 10, 1, 2, 1]
print("Original array:", arr)
sorted_arr = quick_sort(arr)
print("Sorted array:", sorted_arr)

归并排序（Merge Sort）

归并排序也是一种分而治之的排序算法。它的基本思想是将数组分成两个子数组，对这两个子数组分别进行排序，然后将排序后的子数组合并成一个有序的数组。

def merge_sort(arr):
    if len(arr) <= 1:
        return arr

    def merge(left, right):
        result = []
        i = j = 0
        while i < len(left) and j < len(right):
            if left[i] < right[j]:
                result.append(left[i])
                i += 1
            else:
                result.append(right[j])
                j += 1
        result.extend(left[i:])
        result.extend(right[j:])
        return result

    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])
    return merge(left, right)

# 示例使用
arr = [3, 6, 8, 10, 1, 2, 1]
print("Original array:", arr)
sorted_arr = merge_sort(arr)
print("Sorted array:", sorted_arr)

说明

快速排序：
- 选择一个基准元素（pivot）。
- 将数组分成三个部分：小于基准的部分、等于基准的部分和大于基准的部分。
- 递归地对小于基准和大于基准的部分进行排序。
- 合并结果。
归并排序：
- 将数组分成两半。
- 递归地对每一半进行排序。
- 合并两个排序后的子数组。

这两种排序算法都是经典的分而治之算法，具有较好的性能和广泛的应用。

平衡树的数据结构：
- 平衡二叉搜索树（如 AVL 树、红黑树）：这些数据结构在执行插入、删除和查找操作时的递归深度通常是 (O(\log n))，因此在某些实现中，可能会有 (O(\log n)) 的空间复杂度，主要用于递归调用栈。
迭代算法：
- 某些迭代算法在实现中可能会使用一个栈来模拟递归，从而使得其空间复杂度为 (O(\log n))。例如，某些树遍历算法在深度优先搜索时可能使用栈来存储路径信息。

需要注意的是，空间复杂度为 (O(\log n)) 的算法通常涉及递归调用或需要存储某些对数数量的信息。这种复杂度通常与算法的递归深度或树结构的高度相关。

循环与递归在空间复杂度上的差异

def function() -> int:
    # 执行某些操作
    return 0

def loop(n: int):
    """循环的空间复杂度为 O(1)"""
    for _ in range(n):
        function()

def recur(n: int):
    """递归的空间复杂度为 O(n)"""
    if n == 1:
        return
    return recur(n - 1)

函数 loop() 和 recur() 的时间复杂度都为 O(n) ，但空间复杂度不同。

函数 loop() 在循环中调用了 n 次 function() ，每轮中的 function() 都返回并释放了栈帧空间，因此空间复杂度仍为 O(1) 。
递归函数 recur() 在运行过程中会同时存在 n 个未返回的 recur() ，从而占用 O(n) 的栈帧空间。

二、数据结构

数组，链表，栈，队列，哈希表，树，堆，图

@数据结构的物理结构

如图 3-3 所示，物理结构反映了数据在计算机内存中的存储方式，可分为连续空间存储（数组）和分散空间存储（链表）。物理结构从底层决定了数据的访问、更新、增删等操作方法，两种物理结构在时间效率和空间效率方面呈现出互补的特点。

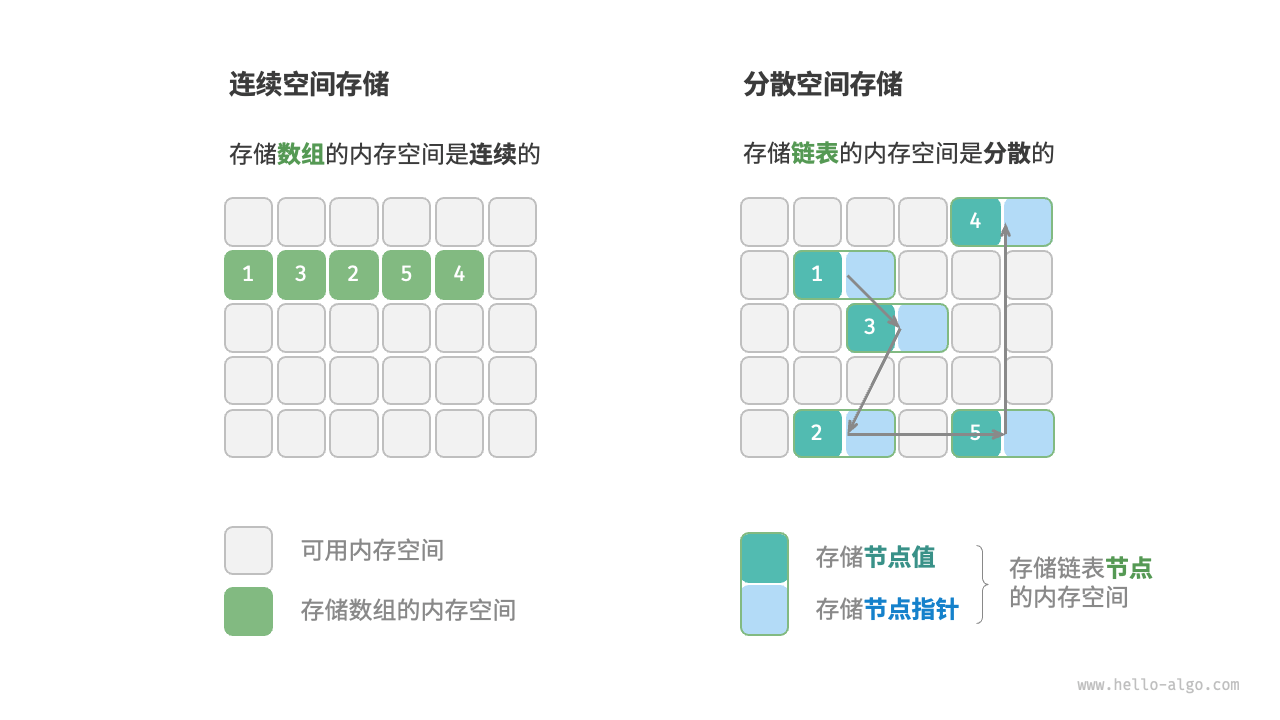
连续空间存储与分散空间存储

连续空间存储（数组）

定义：连续空间存储是指数据元素在内存中连续排列，数组是这种存储方式的典型代表。
优点：
- 快速访问：由于数组元素是连续存储的，可以通过索引直接访问任意元素，时间复杂度为 O(1)。
- 空间局部性：连续存储有助于缓存命中率，因为访问一个元素后，后续访问相邻元素时，可能已经在缓存中。
缺点：
- 插入和删除操作效率低：在数组中插入或删除元素通常需要移动其他元素以保持数据的连续性，时间复杂度为 O(n)。
- 固定大小：数组的大小在创建时确定，扩展数组的大小需要重新分配内存并复制数据。

分散空间存储（链表）

定义：分散空间存储是指数据元素在内存中不必连续排列，链表是这种存储方式的典型代表。
优点：
- 动态大小：链表可以方便地进行动态内存分配，允许在运行时灵活地增加或减少元素。
- 高效插入和删除：在链表中，插入和删除元素只需调整指针，而不需要移动其他元素，时间复杂度为 O(1)（在已知位置的情况下）。
缺点：
- 访问速度慢：由于链表元素存储在非连续的内存位置，访问某个特定元素需要从头遍历链表，时间复杂度为 O(n)。
- 额外空间开销：链表需要额外的存储空间来存储指针（如前驱和后继指针），这增加了内存使用量。

互补特点

数组适合需要频繁随机访问的场景，如需要快速读取大量数据但不经常修改数据的情况。
链表适合需要频繁插入和删除操作的场景，如实现动态数据结构（例如队列、栈）时。

值得说明的是，所有数据结构都是基于数组、链表或二者的组合实现的。例如，栈和队列既可以使用数组实现，也可以使用链表实现；而哈希表的实现可能同时包含数组和链表。

基于数组可实现：栈、队列、哈希表、树、堆、图、矩阵、张量（维度 ≥3 的数组）等。
基于链表可实现：栈、队列、哈希表、树、堆、图等。

哈希表底层是数组，而为了解决哈希冲突，我们可能会使用“链式地址”（后续“哈希冲突”章节会讲）：数组中每个桶指向一个链表，当链表长度超过一定阈值时，又可能被转化为树（通常为红黑树）。

从存储的角度来看，哈希表的底层是数组，其中每一个桶槽位可能包含一个值，也可能包含一个链表或一棵树。因此，哈希表可能同时包含线性数据结构（数组、链表）和非线性数据结构（树）。

Algorithm

#tutorial #C/C++ #Finished #Time and Space Complexity #Recursion #Hello-algorithm-tutorial

Algorithm-Introduction

https://xiyuanyang-code.github.io/posts/Algorithm-Introduction/

Author

Xiyuan Yang

Posted on

November 28, 2024

Updated on

February 17, 2025

Licensed under

Above-All Previous

LaTeX-Tutorial Next

Algorithm-Introduction

Algorithm_tutorial_section1

Algorithm.Section1 Introduction

一、算法 复杂度分析

@迭代与递归

@时间复杂度

@空间复杂度

快速排序（Quick Sort）

归并排序（Merge Sort）

说明

二、数据结构

@数据结构的物理结构

一、算法复杂度分析