Algorithm-BinaryTree

Binary Tree for MIT 6.006

Maybe you just need a binary tree…

graph TD;
    A[5]
    B[3]
    C[8]
    D[2]
    E[4]
    F[7]
    G[9]

    A --> B
    A --> C
    B --> D
    B --> E
    C --> F
    C --> G
    
    

Introduction

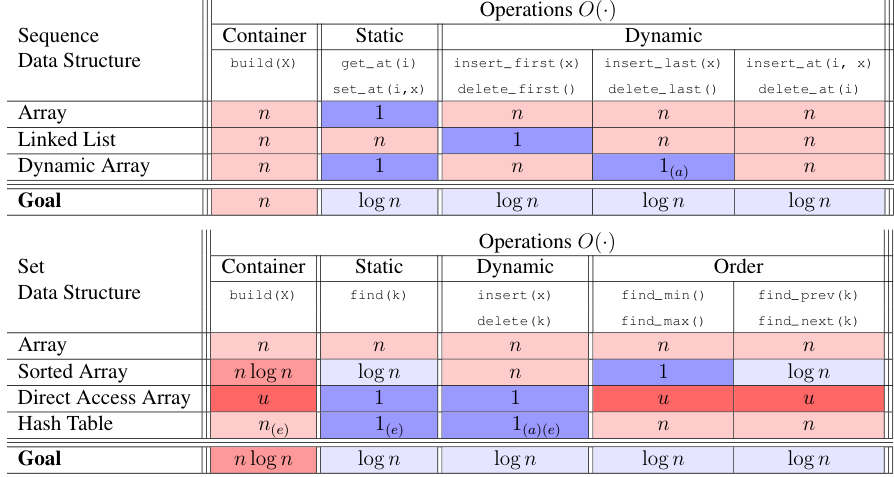
Assume we have discussed Sequence Data Structure and Set Data Structure. Different data structures have different advantages as well as disadvantages.(Linked List and Array, etc) We hope to design a data structure with lower time complexity!

What’s the sacirfices? Maybe the container and space.

We just ignore the basic definition of binary tree! You can go through this blog: Binary Tree.

Thus a node in binary tree needs to store three pointers: parent node, left-child node and right-child node.

Definitions and Terminology

• Subtree
  • We can give the recursive definition of binary tree.
  • subtree of $x$ is $x$ and its descendants. (x to be the root)
• root node, leafs
• depth
  • Every node has unique path from the current node to the root node.
• height
  • the maximum depth of nodes in x’s subtree.
  • the longest road to get to the leaf nodes.

We first ensure all operations shown above is O(h), where h is the height of the root node. We will then try to ensure that $O(h)$ is equinumerous to $O(logn)$ by AVL Tree.

Traversal Order of Nodes

The basic sequence of traversal order: left-root-right.

Algorithm:

iterate(node):
	iterate(node.left)
	node
	iterate(node.right)

The traversal order provides a way to deal with a sequential list of data by binary tree.

Operations

Traversal Operations

subtree_first(node)

Given a subtree (of its node), which comes first in traversal order?

while(node.left != nullptr){
	node = node.left;
}
return node;

• Go left as much as possible!
• When the current node is leaf node or simply has no left node, just undo to the previous layer.
  • The process itself is like a recursion! (Just follow the recursive definition of a tree)

Of course, you can define subtree_last(node).

while(node.right != nullptr){
	node = node.right;
}
return node;

successor(node)

Return the next node after the given node in tree’s traversal order.

Firstly, check whether the right node of this node is empty. If no, then go to its right node and traverse the new subtree formed by its right node, which means return the node of subtree_first(node.right).

If yes, we need to ensure whether its parent node has been traversed. If this node is the left child of its parent node, then just go to the parent node followed by traversal orders. However, if it is the right child of its parent node, we just need to go upper to the parent node of its parent node, until the current node is the left child of its parent node!

if(node.right == nullptr){
	//the right child is empty
	while(node.parent != nullptr && node != node.parent.left){
		node = node.parent;
	}
    return node.parent;
}else{
	return subtree_first(node.right);
}

These operations above just takes $O(h)$, where h is the height of the tree. You just need to check at most one single node in the same layer.

We can also define the predecessor() function to get the previous node similarly.

if(node.left != nullptr){
    return subtree_last(node.left);
}else{
    while(node.parent != nullptr && node.parent.right != node){
        node = node.parent;
    }
    return node.parent;
    
}

Insert and delete

subtree_insert_after(node, new)

Insert the new node new through the traversal order, enabling it to be right before node in the tree.

• If there is no right child: put new there!
  • You just need to “create” a right child of the node node.
• If there is a right child:
  • Then we want the new node to be in the position before node.right. Thus, it needs to be node.right‘s left child!
  • We should return subtree_first(node.right).

if(node.right == nullptr){
	node.right = new;
	new.parent = node;
}else{
	new.parent = subtree_first(node.right);
	subtree_first(node.right).left = new;  
}

subtree_delete(node)

Delete the node without changing other node’s traversal order.

In order to make the tree no to be “crashed“, we first need to get the previous node of the node to be deleted. We can use the predecessor() function which is symmetric to successor() function.

As is shown obviously, deleting a leaf node is very simple, thus we want to exchange the node into the leaf node without breaking the traversal order.

To be more specific, we can understand node as an “invisible” element in the traversal order, which can freely swap positions with other elements without changing the traversal order of the other elements. Ultimately, we hope to move node to the position of a leaf node.

if(node.right == nullptr && node.left == nullptr){
	//is the leaf node
	if(node == node.parent.left){
		node.parent.left = nullptr;
	}else{
        node.parent.right = nullptr;
    }
}else{
    if(node.right != nullptr){
        //then we can go deeper to get to the leaf node!
        while(!(node.right == nullptr && node.left == nullptr)){
            swap(node, predecessor(node));
            //just swap the content 
        }
        delete(node)
    }else{
        //the node only have right child
        //swap items with the successor of <X> and recurse
    }
}

In a word, you just need to go down deeper and deeper, until you reach the leaf node. Then delete it!

Applications

• Sequence: traversal order = sequence order.
• Set: traversal order = increasing item key.
  • Binary search tree.

For example, if you want to find an element in the tree, it’s just like the binary search! (If is bigger than the target, than go right. Else, go left)

For we let the Binary search tree to be sorted strictly by value: node.left.value < node.value < node.right.value. This property of Binary Search Tree (BST) is the key of implementing the time complexity of $O(h)$!

We can also implement find_next() and find_pre().

We have implemented that the time complexity of Binary tree is $O(h)$. Now, think of the question, what is the relation between tree’s height h and the number of nodes n?

• Case 1: This tree is a full binary tree, which means all nodes are saturated (except for the leaf nodes on the bottom layer). In this case, $n$ is strictly $2^h-1$.
• Case 2: A singly linked list is a degenerate binary tree, where the height $h$ of the tree equals the number of nodes $n$.

Thus, we have

$$2^h-1 \ge n \ge h$$

graph TD;
    A[1]
    B[2]
    C[3]
    D[4]
    E[5]
    F[6]
    G[7]

    A --> B
    A --> C
    B --> D
    B --> E
    C --> F
    C --> G

graph TD;
    A[1]
    B[2]
    C[3]
    D[4]
    E[5]

    A --> B
    A --> null1[null]
    B --> C
    B --> null2[null]
    C --> D
    C --> null3[null]
    D --> E
    D --> null4[null]
    E --> null5[null]
    E --> null6[null]

subtree_at(node, i)

subtree_at(node, i) requires a node and the index i (0-based), asking to find the ith node in the subtree of node.

We first assume we have already known the size(node) function which can return the number of nodes in the node‘s subtree. Then we can implement this algorithm.

int nL = size(node.left);
//this is the index of node in the subtree
if(i < nL){
    //find the node recursively!
    //for it's in the left tree, thus the index of the subtree of node and the index in the subtree of node.right is equal.
    return subtree_at(node.left,i);
}else if(i == nL){
    return node;
}else{
    //i > nL
    return subtree_at(node.right, i-nL-1);
    //i - nL -1 is the new index in the subtree of node.right. 
}

Subtree augmentation

• each node can store $O(1)$ extra fields/properties.
• node.size = node.left.size + node.right.size + 1
• Subtree property (node) can be computed from properties of node’s children (and node) in $O(1)$ time.

However, if you don’t have any information, computing the size of a subtree achieves $O(n)$ time complexity. (You just need to go through all nodes recursively!) So we need to sacrefice the space: for every node, we have a private member called node.size. Then we should update this variable no matter what operations are.

For insertion and deletion, we ultimately add a leaf node in the tree. We need to modify all nodes that are ancestors of the added node. It;s also $O(h)$ time complexity.

while(node != nullptr){
	node.size ++;
    node = node.parent;
}

Subtree properties

• sum, product, min, max of some features of every node in subtree.
• index in the traversal order is not the properties that need to be maintained because modifications may change all node’s indexes.

Part2: AVL Tree

We now need to bound $h$ to $log(n)$!

Definitions: Balanced Binary Tree is a tree that enjoys $h=log(n)$.

A more strict definition: We define the skew of the node:

$$\left | height(node.left)-height(node.right) \right |\le 1 $$

Rotation

We want to modify the tree in a way that doesn’t modify it in traversal order. That is rotation, including right rotation and left rotation.

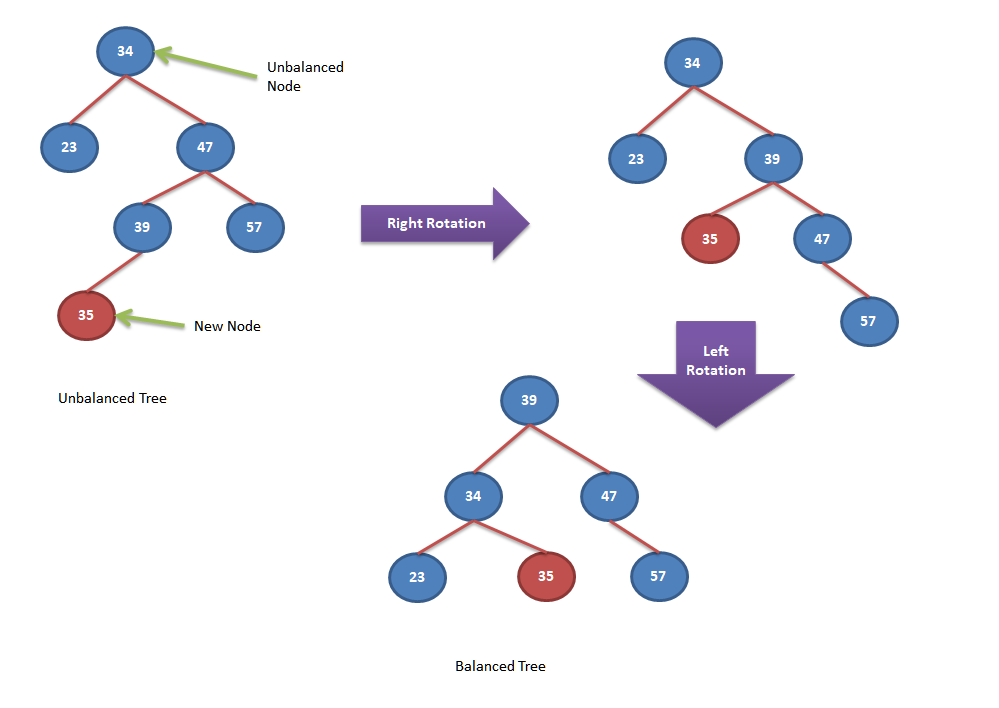
During the process shown above, we can get to manipulate the tree from an unbalanced tree into a balanced tree.

Balanced Tree

All balanced Trees have a logarithmic time complexity.

We consider the worst balanced tree, which all nodes of the left subtree has the height of h-2, while all nodes of the right subtree has the height of h-1.(The total height, including the root node, is h).

Then we suppose $N_{h}$ is the number of nodes in this tree (height of the tree is h), Then we can solve this case using a recursive equation:

$$N_{h} = N_{h-1} + N_{h -2} + 1$$

Then is the boring math… We can just skip that part and we can prove that All balanced Trees have a logarithmic time complexity.

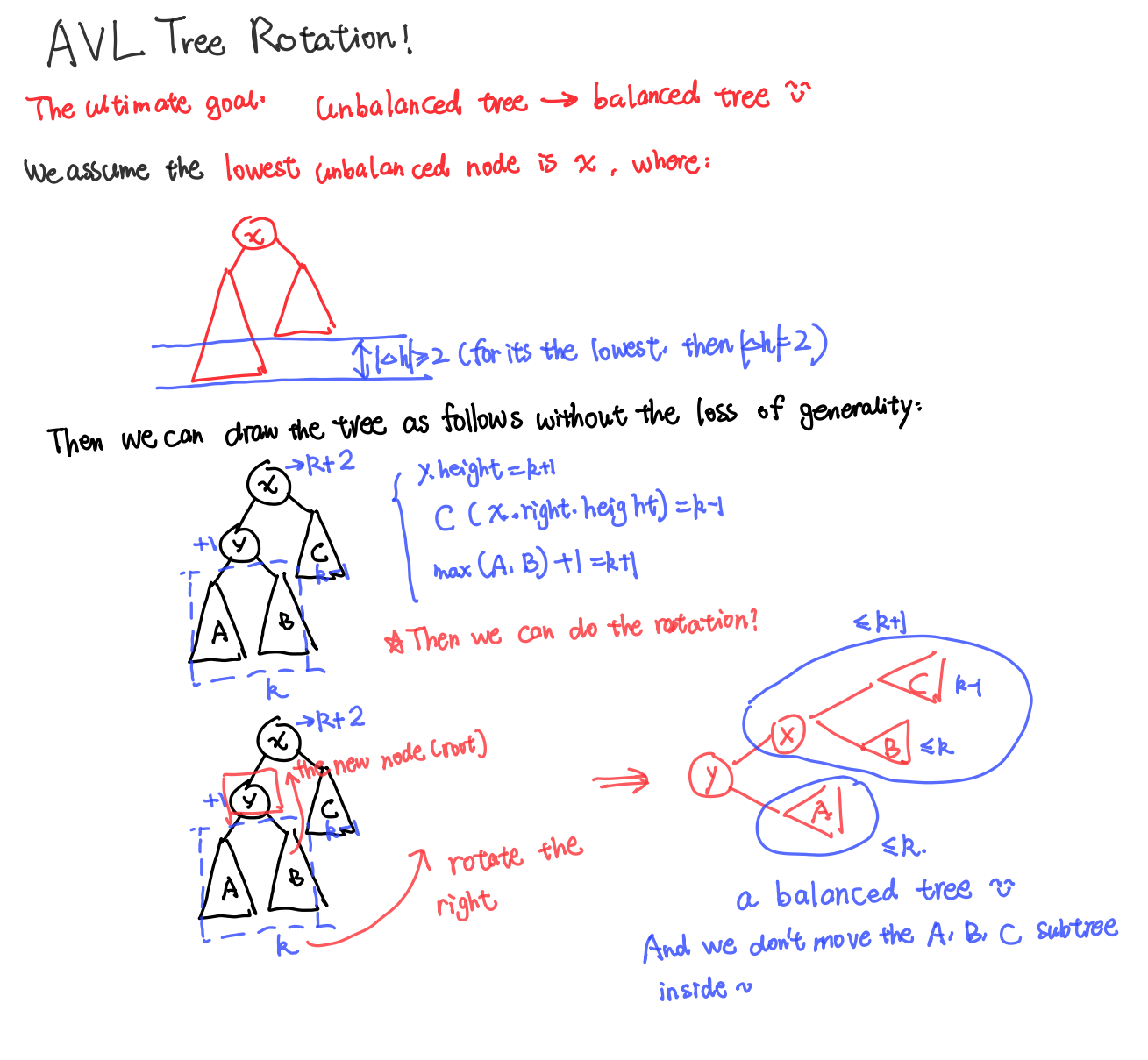
Height and the unbalanced…

Consider the lowest unbalanced node $x$. We want to build a balanced tree where all nodes enjoys the property of $\left | height(node.left)-height(node.right) \right |\le 1 $ or we can say $ height(node.left)-height(node.right) \in { 1,0,-1 }$.

Now we know the node $x$ doesn’t enjoy the property above. Moreover, due to it is the lowest unbalanced node, the out of range situation will only be $-2$ or $2$.

Hence, we have properties below: $$height(node.left)-height(node.right) \in {2 , -2 }$$

Without the loss of generality, we just assume that $height(node.left)-height(node.right) = 2$!

graph TD
    A((A)) --> B((B))
    A --> C((C))
    B --> D((D))
    B --> E((E))
    D --> F((F))
    D --> G((G))

Then we suppose the left child of node $x$ is $y$. Then we have three subtrees, where they are: the right subtree of node $x$ and the left and the right subtree of node $y$. If we assume $x.right.height = k-1$, then $x.left.height = k+1$ and $x.height = max(x.left.height, x.right.height) + 1 = k+2 $. And for the subtree of $x.left$, there are three possibilities:

• $x.left.left.height =x.left.right.height + 1 = k +1$: Then we can just rotate the node $y$ into the balanced tree!
• $x.left.left.height =x.left.right.height = k +1$: The situation is just the same!
• $x.left.left.height + 1 =x.left.right.height = k +1$

For the first two questions, you can see the demo shown below:

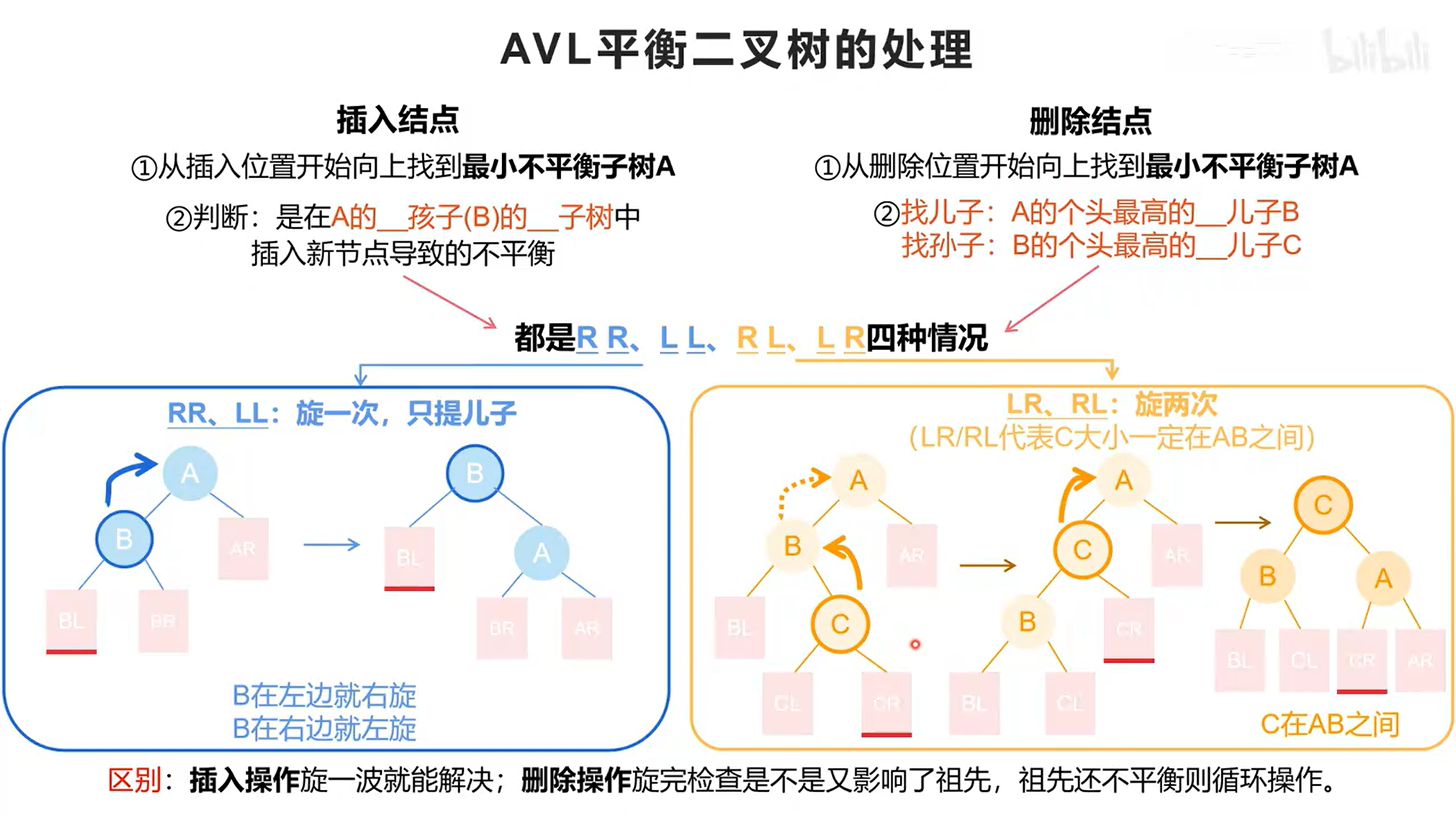
For case 3, it’s a little bit harder! We can just see this picture shown previously:

In this case, we will operate two operations totally. Firstly, we will right rotate the node $39$ (Just like the operations in the other two cases). Secondly, we will left rotate the node $47$, and it will become a balances tree!

If you want to memorize this:

Video Clip: AVL balanced Tree

Conclusion

In the first section, we talk about the basis of Binary Tree, regarding several operations like delete and insert a node and the traversal order of the binary tree. Why we need to do this, because the special storage of binary tree ensures all operations is within the time limit of $O(h)$, and the sequence of traversal ensures the relations of a sequential list and a binary tree. (For the set structure, we have BST)

In the second part, we need to ensure $O(h) \equiv O(logn)$.If we don’t do anything, there are some bad situations (like the singly linked list) where $O(h)=O(n)$. To avoid this situation, we need to rotate the binary tree to a balanced tree to make the $O(h) \equiv O(logn)$ is true without changing the traversal order of the binary tree.