AINN Transformer
Transformer (is all you need?)
Introduction
今天来讲最经典的网络结构：Transformer！！！
Preliminaries
在理解这个任务之前，我们首先需要读懂摘要中的第一句话：The dominant sequence transduction models are based on complex recurrent or convolutional neural networks that include an encoder and a decoder. 因此，我们首先需要解释相关概念：
- Sequence transduction models
- Recurrent Neural Networks
- Convolutional Neural Networks
- 卷积神经网络，这个其实相对不那么重要，check This Blog for more details.
- Encoder and Decoder
Sequence Transduction Model (Seq2Seq)
Transformer最开始的论文（Attention is all you need）的任务其实是聚焦在Machine Translation上的，这个在摘要部分也能很清晰的看见：
Our model achieves 28.4 BLEU on the WMT 2014 English-to-German translation task, improving over the existing best results, including ensembles, by over 2 BLEU. On the WMT 2014 English-to-French translation task, our model establishes a new single-model state-of-the-art BLEU score of 41.8 after training for 3.5 days on eight GPUs, a small fraction of the training costs of the best models from the literature.
而进行语言翻译工作的模型就是一个非常典型的序列转导模型（Sequence transduction models），即其主要目标是将输入序列转换为输出序列。（在这里输入序列就是待被翻译的文字序列，而输出序列就是被翻译出来的文字序列）
而深度学习最经典的操作就是Embedding，在这里每一个词都会被映射为一个高维的向量，假设其维度为$d_m$，并且我们假设输入序列有$T$个词，则输入矩阵$\in \mathbb{R}^{T\times d_m}$。因此，序列转到模型本质上就是从一个矩阵生成另一个矩阵。
$$M \in\mathbb{R}^{T_1 \times d_m} \to \boxed{\text{Sequence transduction models}} \to N \in \mathbb{R}^{T _2\times d_m}$$
其中$T_1$是输入序列的长度，而$T_2$的输出序列的长度，$d_m$是每一个token embedding的维度。
Recurrent Neural Networks
Recurrent Neural Networks，循环神经网络，是在当时处理序列预测问题的主流模型框架，其想法也非常简单：依照时序预测的顺序，$t$时刻的状态$h_t$由$t-1$时刻的状态$h_{t-1}$和$t$时刻的输入$i_t$决定。最经典的循环神经网络架构比如说LSTM。
RNN的想法很简单也很直观，但是存在几个非常严重的问题：
- RNN的预测是依赖于之前的状态的，换句话说，$h_t$的生成需要保证$h_{t-1}$的序列预测完成，这在面对长上下文处理的任务是会显得非常的迟钝和低效率，并且无法发挥GPU在并行任务上的优势。
- RNN的网络结构非常复杂，训练需要的计算开销和损失都很大，并且很容易出现梯度消失的现象。
- 遗忘问题：对于较长的序列预测来说，由于上一阶段的状态是不断更新的，这就很容易导致模型学了前面的忘了后面的，即早起序列信息的遗忘问题。
Encoder and Decoder
Autoencoder
自编码器（Autoencoder）是一种无监督学习模型，主要用于数据降维、特征学习和数据重构。自编码器的基本结构包括编码器和解码器两个部分。以下是自编码器的简单介绍：
编码器（Encoder）
- 编码器的任务是将输入数据（如图像、文本等）转换为一个低维的潜在表示（latent representation），通常称为编码（code）或瓶颈（bottleneck）。(Embeddings)
- 编码器通过一系列神经网络层（通常是全连接层或卷积层）逐步减少输入的维度。
解码器（Decoder）
- 解码器的任务是将潜在表示转换回原始数据的重构版本。
- 解码器通常与编码器对称，通过一系列神经网络层逐步增加维度，最终输出与输入相同维度的数据。
自编码器的训练目标是最小化输入数据与重构数据之间的差异，常用的损失函数是均方误差（MSE）或交叉熵（Cross-Entropy）。通过反向传播算法，模型学习编码和解码的权重，以提高重构的准确性。
使用数学表示，我们假设输入序列$\mathbf{x} = (x_1,x_2,x_3, \dots x_n)$，则Encoder的架构会将其转化为$\mathbf{z} = (z_1, z_2,z_3,\dots z_n)$。（Embedding的过程），而Decoder完成从$\mathbf{z}$到输出序列$\mathbf{y} = (y_1, y_2, y_3, \dots, y_m)$。
Problems
和RNN面临着相同的问题。
Model Architecture
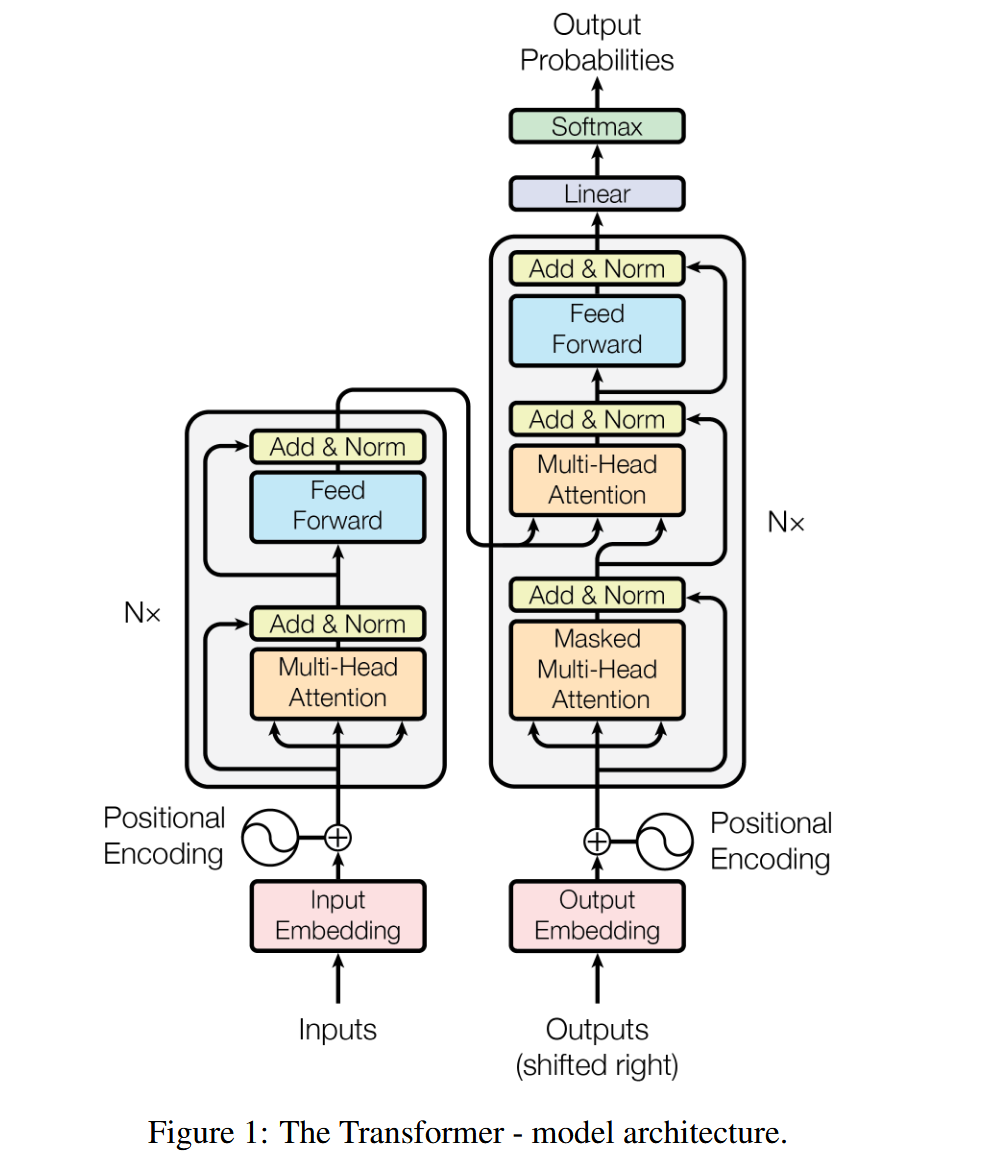
下面来到文章中最关键的部分！我们将逐步拆解Transformer的网络结构。
Overall Architecture
Input and Output
Transformer的整体网络结构仍然保留了Encoder-Decoder的网络结构。因此输入是一个$(batch \times features \times sequence)$的三维张量，经过位置编码之后（Positional Encoding）之后进入编码器。而解码器会接受（目标序列的Embeddings）和编码器的输出，不过为了保证模型的正确性，Output Embeddings需要先做一个掩码（Masked），再进行输入。
在Transformer训练的过程中，是可以看到完整的目标序列的，但是我们希望Transformer不可以未卜先知，而是应该根据之前的内容做预测，因此会采用掩蔽矩阵来消除后续词的影响。
最终解码器经过一个Linear层调整size并通过softmax输出最终归一化的概率。
对于训练过程，目标序列y是已知的，因此我们需要使用掩码来防止模型在训练过程中未卜先知，只能利用之前的生成序列。而对应生成过程，我们不知道目标序列，因此需要模型根据自己之前的生成加上编码器的新的输出来做预测。
Encoder and Decoder
首先，其采用了类似于ResNet的堆叠模式（$N = 6$）。下面只对对一个单元层进行分析：
在Encoder部分，我们可以看到两个子模块，第一个子模块是Multi-Head Attention(是用来模拟卷积神经网络的多通道特征学习来达到并行的目的，后面会详细介绍)，第二个子模块是标准的全连接前馈神经网络。
不过在每一个子模块内，又加入了residual connection（ResNet）并且做了归一化的处理（LayerNorm）。
对于解码器也是类似的结构，不过加了一个Masked MultiHead Attention的结构来防止模型看到后面的预测序列。
Attention is all you need
接下来我们来解释Transformer最核心的模块：多头注意力机制
Scaled Dot-Product Attention
来看下面的例子：
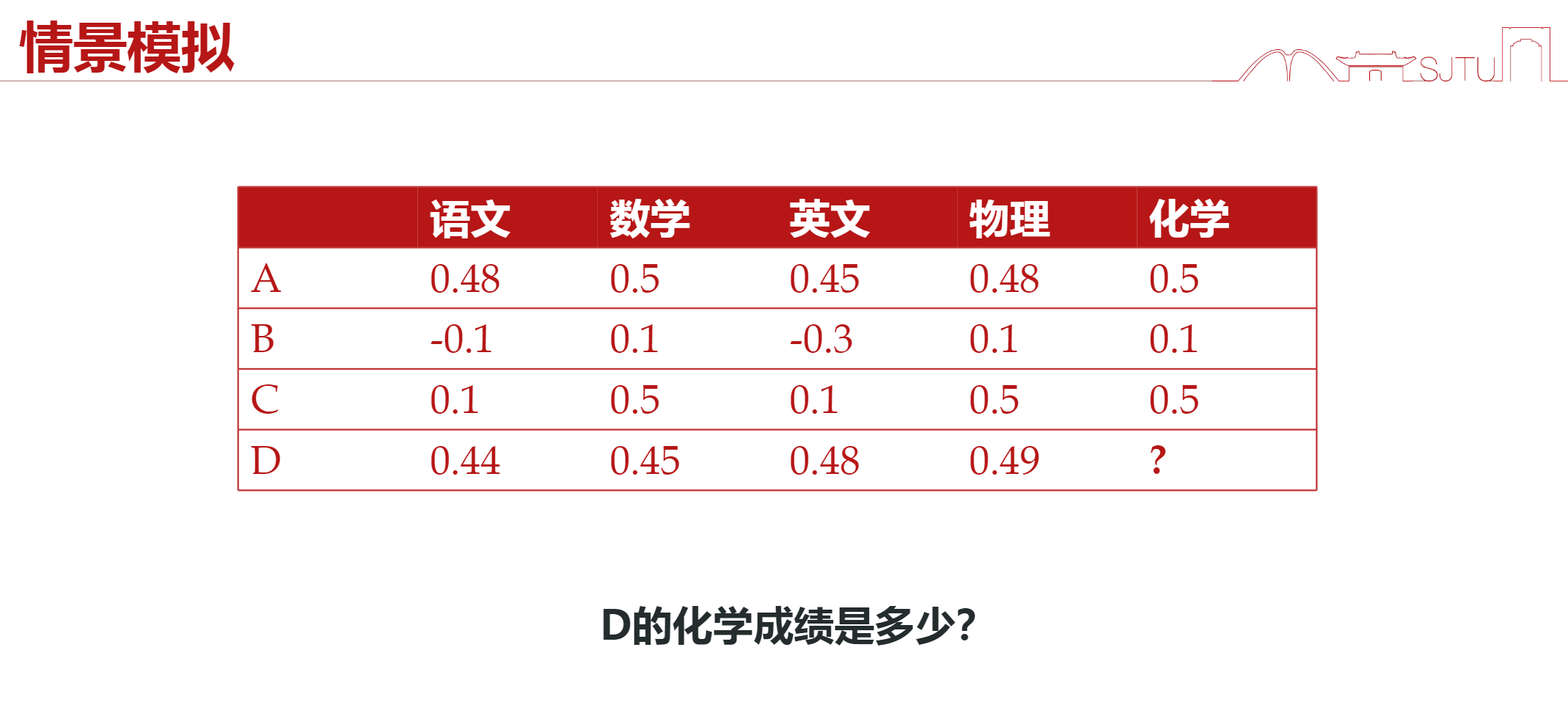
我们需要根据ABC三人的成绩和D剩下四门的成绩来判断D所缺失的化学成绩。
Intuition：根据D其他几门课的成绩判断其在班级中的大概位次，再根据和他成绩差不多同学的化学成绩来拟合他的化学成绩。
如果使用矩阵和向量的形式给出，我们可以给出一个查询矩阵Query（因为这里只涉及到一个查询，因此这里也是一个向量）：
$$Query_D = (0.44, 0.45, 0.48,0.49)$$
接下来，我们需要尽可能的找到在前四门中分数和D尽可能接近的同学，很明显可以转化为一个计算向量余弦相似度的问题，我们可以给出如下的Key向量：
$$Key_A = (0.48, 0.5, 0.45, 0.48)$$
$$Key_B = (-0.1, 0.1, -0.3, 0.1)$$
$$Key_C = (0.1, 0.5, 0.1, 0.5)$$
计算这三个Key向量和之前查询向量的余弦相似度：
$$\text{Cosine Similarity} = \frac{A ·B}{||A|| \times ||B||}$$
我们假设对应的Key向量已经做了归一化处理，那这个时候我们只需要计算点积就可以判断哪一个同学和D最相似！
这样，我们就可以得到一个权重向量，经过softmax之后成为$Query_D$的Attention。
$$Att = [0.48, 0.18, 0.34]$$
Attention代表的是每一个已知的数据点和新的数据点的相似程度，也可以说是新的数据点对不同的已知的数据点的关注程度。因此顺理成章的做一次加权，对什么做加权？对已知数据点的Value（已知的化学成绩）做加权，即：
$$Value = (0.5, 0.1, 0.5)$$
$$\text{prediction} = Value \cdot Att = 0.43$$
现在我们尝试把这个场景给一般化：
我们假设需要翻译的词已经被embedding成了一个高维向量$\mathbb{y} = (y_1,y_2,\dots, y_m)$，这就是我们的已知信息，也就是查询矩阵